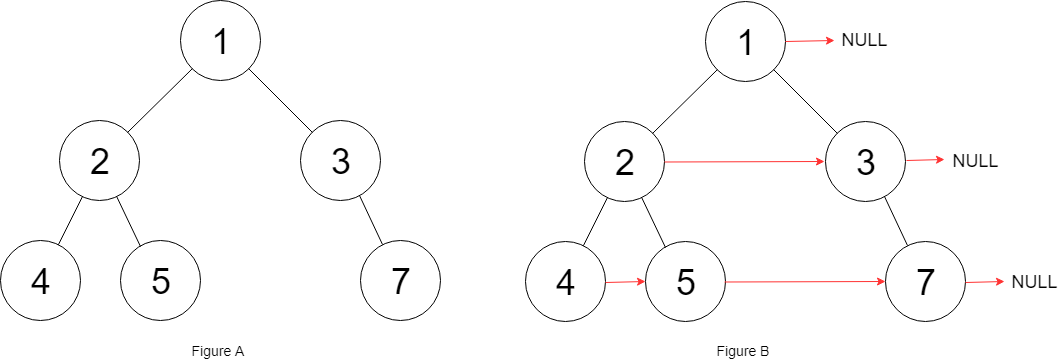
二叉树的前序、中序、后序遍历本质上就是将打印语句放到 “第一次来到该节点、第二次回到该节点、第三次回到该节点” 的位置。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 public static void traversal (Node head) if (head == null ) { return ; } traversal(head.left); traversal(head.right); }
前序遍历:头 -> 左 -> 右
1 2 3 4 5 6 7 8 public static void preOrderRecur (Node head) if (head == null ) { return ; } System.out.print(head.value + " " ); preOrderRecur(head.left); preOrderRecur(head.right); }
后序遍历的非递归方式需要借助两个栈,步骤和前序遍历相似,只不过将一个栈中的元素压入到另一个栈后再统一出栈打印
非递归的前序遍历,需要使用一个栈结构。
先将根节点入栈,然后不断循环,按照 “弹栈打印 -> 右孩子入栈 -> 左孩子入栈” 的顺序遍历,即可实现前序遍历。
因为每次都将右孩子先入栈,同时弹出左孩子时就立刻再次压入其右孩子和左孩子,所以某个节点的右子树会堆积在栈底,一直到其左子树都弹栈后才会再遍历,从而达到了先序遍历的效果。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 public static void preOrderUnRecur (Node head) if (head != null ) { Stack<Node> stack = new Stack<>(); stack.push(head); Node cur = null ; while (!stack.isEmpty()) { cur = stack.pop(); System.out.print(cur.value + " " ); if (cur.right != null ) { stack.push(cur.right); } if (cur.left != null ) { stack.push(cur.left); } } } }
中序遍历:左 -> 头 -> 右
1 2 3 4 5 6 7 8 public static void inOrderRecur (Node head) if (head == null ) { return ; } inOrderRecur(head.left); System.out.print(head.value + " " ); inOrderRecur(head.right); }
思路:把整棵树按照左边界进行分解 ,同时右孩子节点也按照左边界分解,将右子树的节点也依次左孩子节点入栈。即每打印一个节点后就把右子树的节点也依次左孩子节点入栈 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 public static void inOrderUnRecur (Node head) if (head != null ) { Stack<Node> stack = new Stack<>(); while (!stack.isEmpty() || head != null ) { if (head != null ) { stack.push(head); head = head.left; } else { head = stack.pop(); System.out.print(head.value + " " ); head = head.right; } } } }
后序遍历:左 -> 右 -> 头
1 2 3 4 5 6 7 8 public static void posOrderRecur (Node head) if (head == null ) { return ; } posOrderRecur(head.left); posOrderRecur(head.right); System.out.print(head.value + " " ); }
后序遍历的非递归方式需要借助两个栈,步骤和前序遍历相似,只不过将一个栈中的元素压入到另一个栈后再统一出栈打印。
非递归的后序遍历,需要使用两个栈结构,另一个栈用于存储第一个栈弹出的节点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 public static void posOrderUnRecur1 (Node head) if (head != null ) { Stack<Node> stack1 = new Stack<>(); Stack<Node> stack2 = new Stack<>(); Node cur = head; stack1.push(head); while (!stack1.isEmpty()) { cur = stack1.pop(); stack2.push(cur); if (cur.left != null ) { stack1.push(cur.left); } if (cur.right != null ) { stack1.push(cur.right); } } while (!stack2.isEmpty()) { System.out.print(stack2.pop().value + " " ); } } }
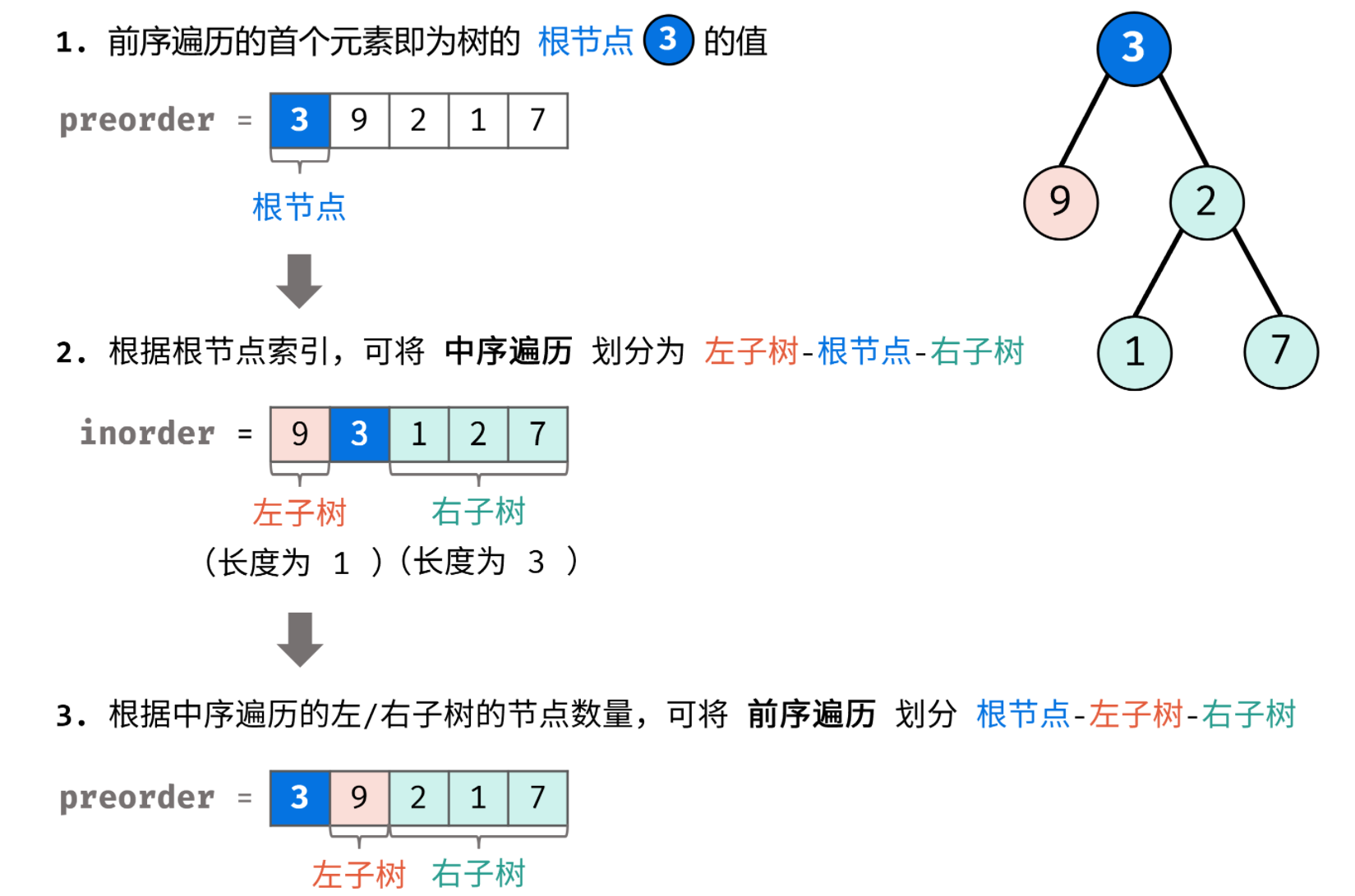
知道前序 遍历序列和中序 遍历序列,可以唯一确定一颗二叉树
知道后序遍历序列和中序 遍历序列,可以唯一确定一颗二叉树
但是只知道后序和前序无法唯一确定一棵二叉树,因为需要中序序列中定位到根节点的位置 才可以进行左右侧划分,否则不知道前序或后序序列中左右子树的划分边界
根节点位置:
前序遍历:在数组的第一个 位置
中序遍历:在数组的中间某个 位置(第一个位置为整棵树最左侧的节点)
后序遍历:在数组的最后一个 位置
左右子树的分布特点:
前序遍历:根 -> 左 -> 右
中序遍历:左 -> 根 -> 右
后序遍历:左 -> 右 -> 根
具体分布可见下图:
相关题目可见:重建二叉树 与二叉搜索树的后续遍历序列 。
层次遍历常用于和树的宽度 相关或需要知道当前节点所在层信息 的题目,例如求树的最大宽度,或者判断完全二叉树。
层次遍历常常与队列一起组合出现 ,因为使用队列先进先出的特点才能保证做到层次遍历,如果是栈结构的先进后出,就无法做到层次遍历。
层次遍历的一个技巧,可以在进入每层后,首先获取队列中节点的个数,其就代表了当前层的节点数目,那么就可以在开启一个内层 while 循环,一次性遍历当前层的所有节点。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 public void levelOrder (Node head) if (head == null ) return ; Queue<Node> queue = new LinkedList<>(); queue.add(head); while (!queue.isEmpty()) { int size = queue.size(); while (size-- > 0 ) { Node cur = queue.poll(); System.out.println(cur.value); if (cur.left != null ) queue.add(cur.left); if (cur.right != null ) queue.add(cur.right); } } }
之字形遍历即要求奇数层从左往右打印,偶数层从右往左打印。要实现该功能,有三种思路:
仍然采用传统的层次遍历,只不过在最后对偶数层集合进行逆序 ;或在偶数层添加元素时从后往前加入到结果集合 LinkedList<>#addLast() 中
使用两个栈结构 。一个栈存储奇数层的节点,一个栈存储偶数层的节点
遍历奇数层时,向偶数栈中压入当前层的孩子;先左后右
遍历偶数层时,向奇数栈中压入当前层的孩子;先右后左
使用一个双端队列 结构。每次不止遍历两层,而是先遍历奇数层,再遍历偶数层
奇数层是从头出,从尾入;先左后右
偶数层是从尾出,从头入;先右后左
注意:出和入的方向肯定是相反的,不然就会导致刚入的,就要出了
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 public List<List<Integer>> levelOrder(TreeNode root) { if (root == null ) { return new ArrayList<>(); } return levelOrderDeque(root); } public List<List<Integer>> levelOrderTwoStack(TreeNode root) { List<List<Integer>> res = new ArrayList<>(); Stack<TreeNode> stackOdd = new Stack<>(); Stack<TreeNode> stackEven = new Stack<>(); stackOdd.push(root); while (!stackOdd.isEmpty() || !stackEven.isEmpty()) { List<Integer> list = new ArrayList<>(); if (!stackOdd.isEmpty()) { while (!stackOdd.isEmpty()) { root = stackOdd.pop(); list.add(root.val); if (root.left != null ) { stackEven.push(root.left); } if (root.right != null ) { stackEven.push(root.right); } } } else { while (!stackEven.isEmpty()) { root = stackEven.pop(); list.add(root.val); if (root.right != null ) { stackOdd.push(root.right); } if (root.left != null ) { stackOdd.push(root.left); } } } res.add(list); } return res; } public List<List<Integer>> levelOrderDeque(TreeNode root) { Deque<TreeNode> queue = new LinkedList<>(); List<List<Integer>> res = new ArrayList<>(); queue.addFirst(root); while (!queue.isEmpty()) { int size = queue.size(); List<Integer> list = new ArrayList<>(); while (size-- > 0 ) { root = queue.removeFirst(); list.add(root.val); if (root.left != null ) { queue.addLast(root.left); } if (root.right != null ) { queue.addLast(root.right); } } res.add(list); if (!queue.isEmpty()) { size = queue.size(); list = new ArrayList<>(); while (size-- > 0 ) { root = queue.removeLast(); list.add(root.val); if (root.right != null ) { queue.addFirst(root.right); } if (root.left != null ) { queue.addFirst(root.left); } } res.add(list); } } return res; }
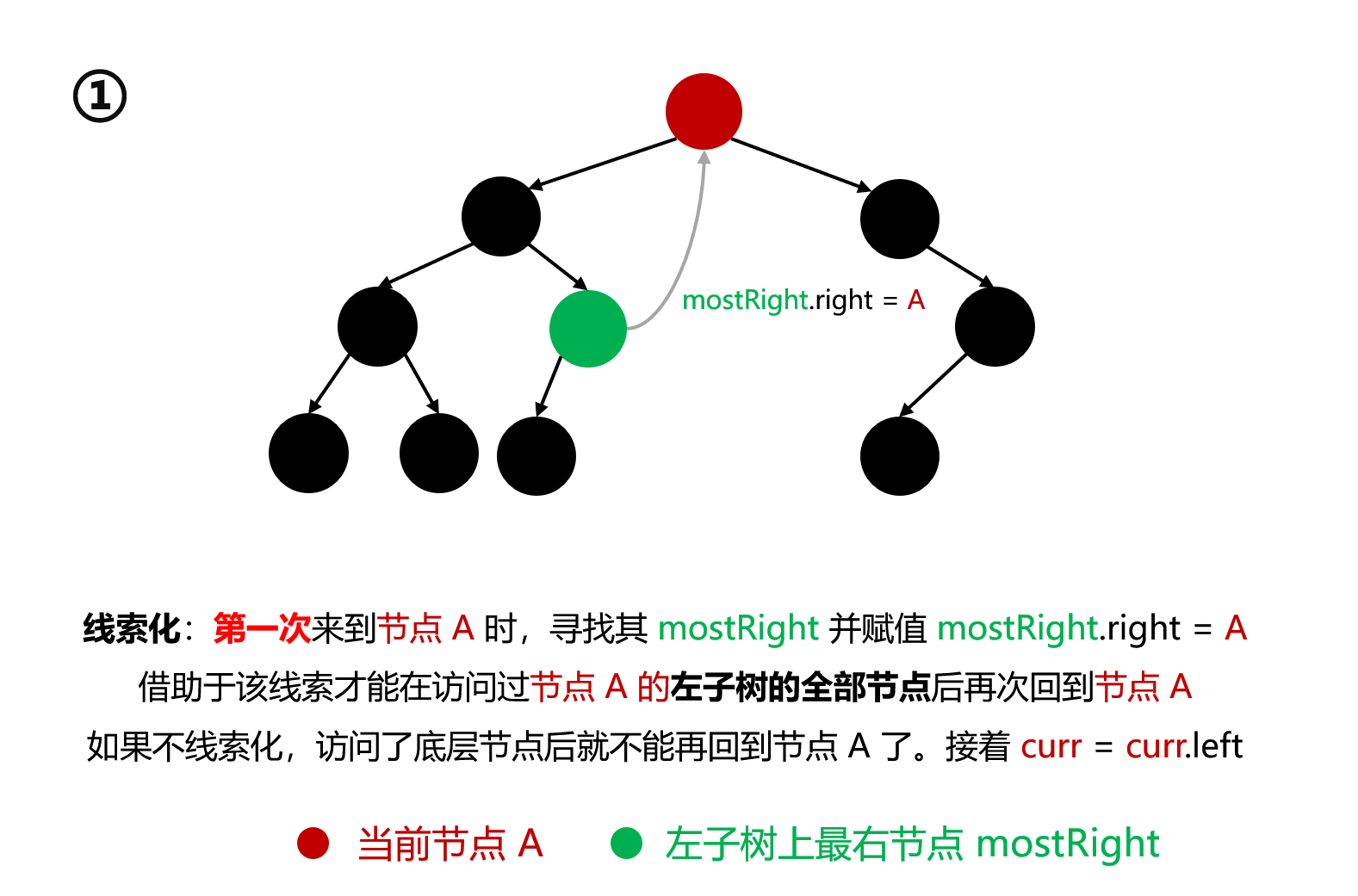
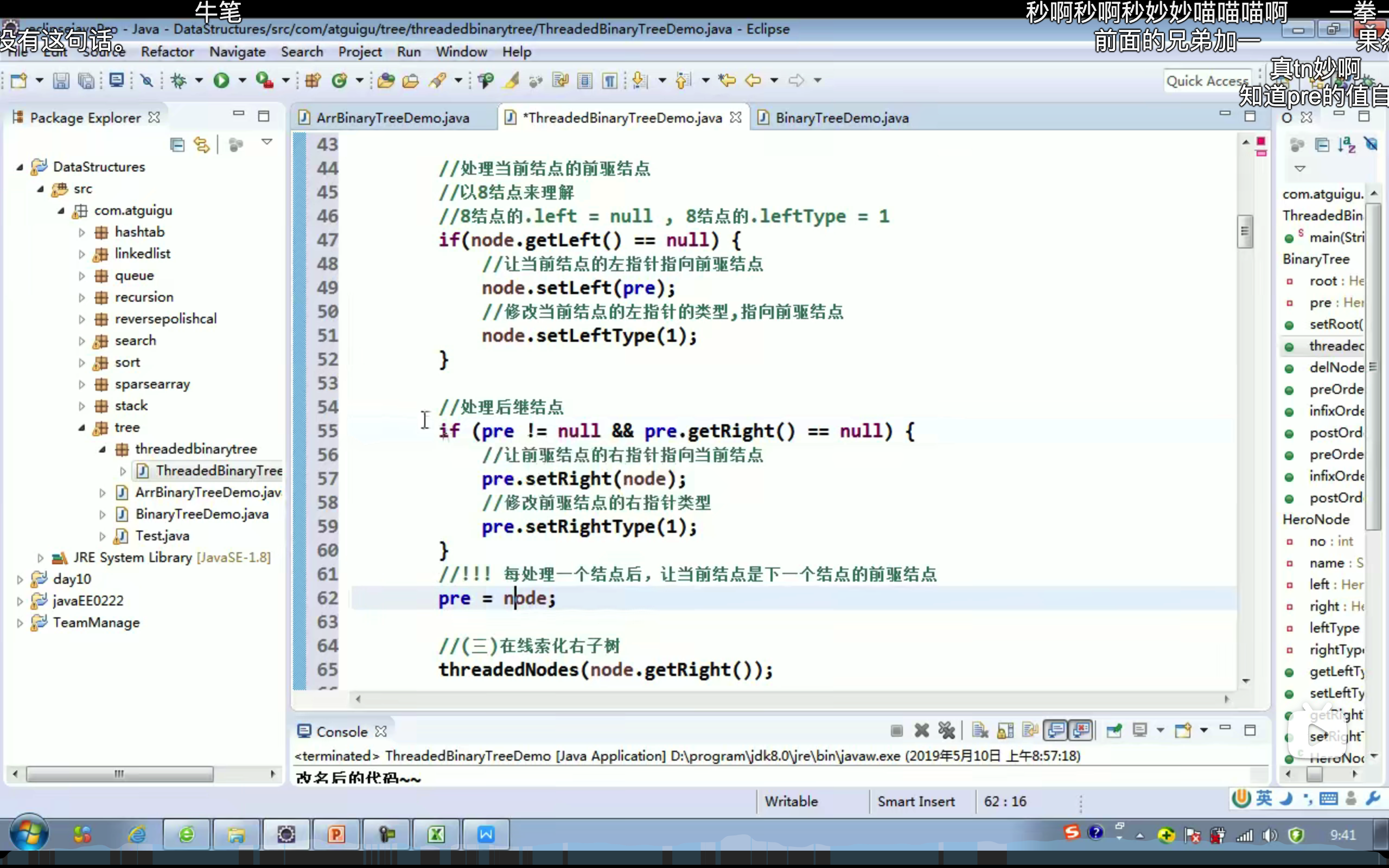
假设来到当前节点 cur,开始时 cur 在头节点位置
如果 cur 没有左孩子,则 cur 向右移动 cur = cur.right(这里会因为事先建立的线索而再次回到上层节点)
如果 cur 有左孩子,找到 cur 的左子树上的最右侧节点 mostRight:
如果 mostRight 的右指针指向空(说明是第一次到该节点,还没建立线索),让其指向 cur(mostRight.right = cur),此时建立了当前节点左子树最右节点与当前节点间的线索 。然后 cur 向左移动 cur = cur.left,开始向左子树遍历
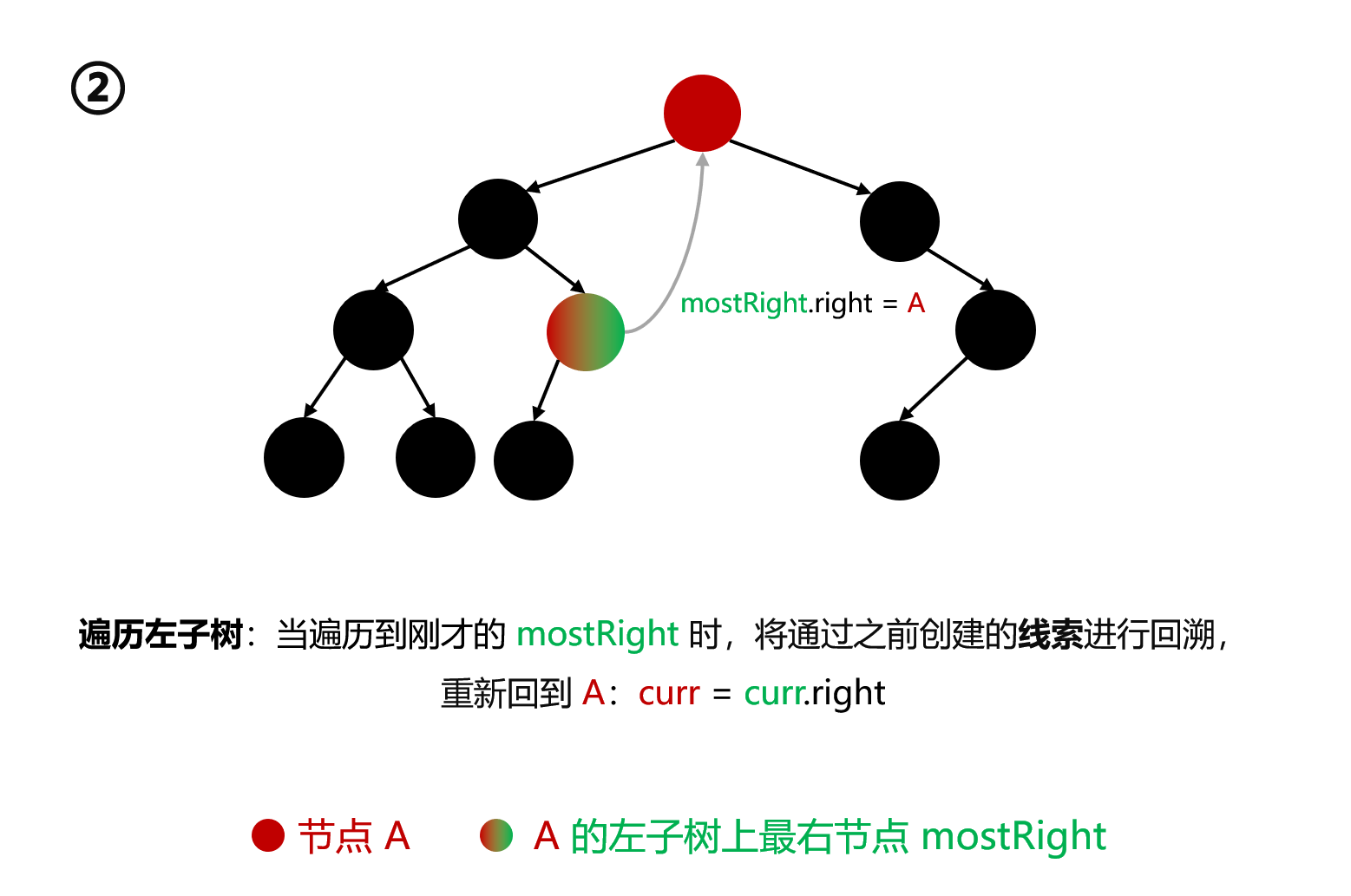
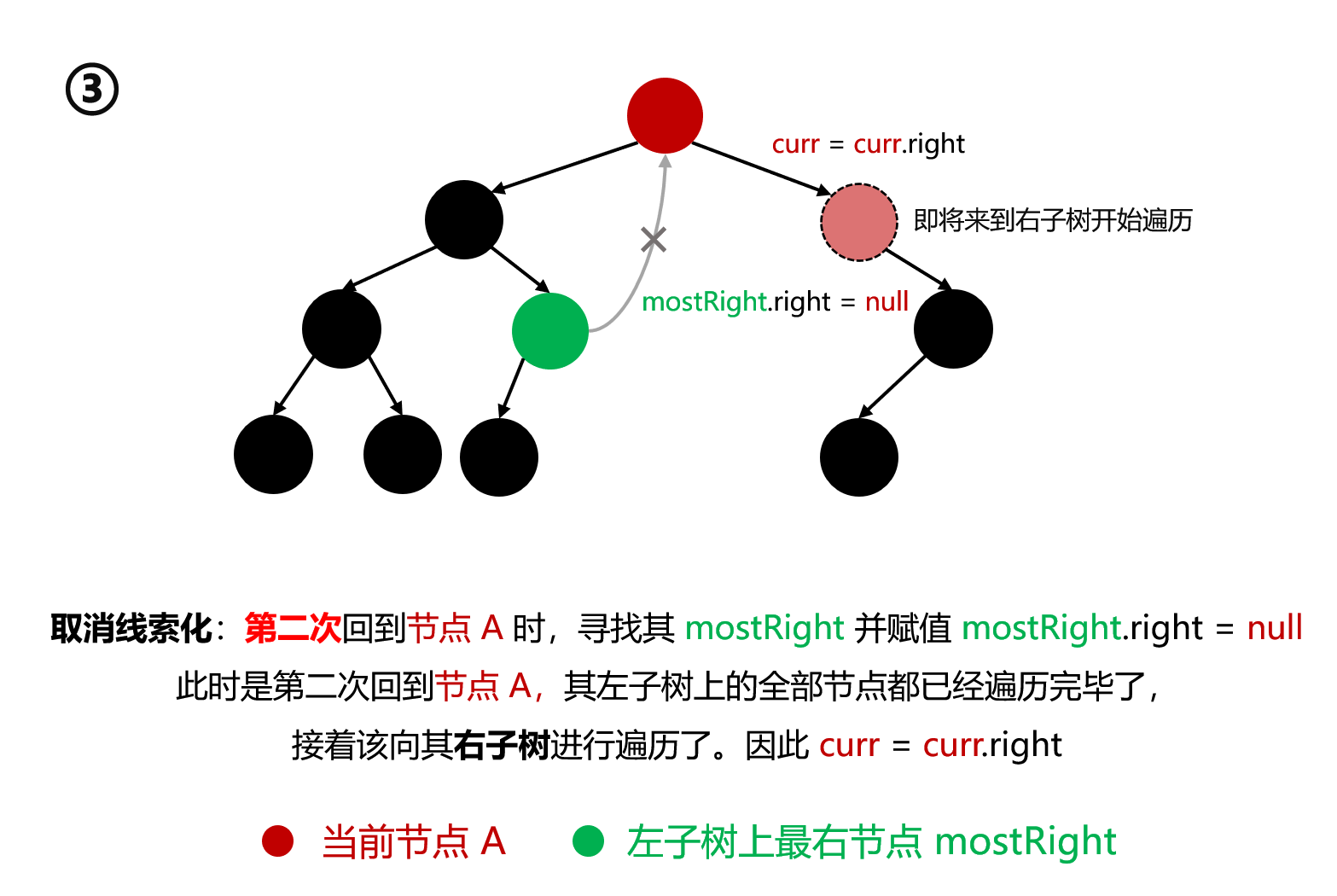
如果 mostRight 的右指针指向 cur(说明是第二次到该节点,之前就建立过线索了),让其指向 null(取消线索),断开了之前建立的线索,恢复了最右节点的原始结构。然后 cur 向右移动 cur = cur.right。开始向右子树遍历
cur 为 null 时遍历停止
上述流程可分为三个阶段:
线索化 :第一次来到某节点 A,寻找其 mostRight 并赋值 mostRight.right = A。借助于该线索才能在访问过节点 A 的左子树的全部节点 后再次回到节点 A。如果不线索化,访问了底层节点后就不能再回到节点 A 了。接着 cur = cur.left,即开始向左子树遍历 遍历左子树 :A 完成线索化后,开始向左子树遍历。当遍历到刚才的 mostRight 时,将通过之前创建的线索 进行回溯,重新回到 A:cur = cur.right取消线索化 :第二次 回到节点 A 时,寻找其 mostRight 并赋值 mostRight.right = null。此时是第二次回到节点 A,其左子树上的全部节点都已经遍历完毕了,接着该向其右子树 进行遍历了。因此 cur = cur.right
上述三个阶段的图示:
建立线索——消除线索的过程:
开始时所有子树的最右节点的 right 都是 null,此时还没建立起线索
接着第一次 来到某个节点 A 时,若其左子树的最右节点存在,则会建立该最右节点与当前节点的线索 ,具体方法是:mostRight.right = A。然后当前节点继续向左移动:cur = A.left。注意:这里建立的线索将会在后续遍历到 mostRight 节点时,执行 cur = mostRight.right 语句来再次回到节点 A
当 cur 在向左子树不断遍历的过程中来到刚才建立线索的最右节点 mostRight 时,会执行 cur = mostRight.right 语句重新回到其线索指向的祖先节点 A,从而做到了第二次 回到节点 A
第二次回到节点 A 后,继续寻找其左子树上的最右节点 mostRight,然后取消线索化:mostRight.right = null,从而恢复其原始结构
线索化的目的 :在访问了底层节点后,依旧能借助该线索再次回到上层的节点,从而继续向右侧迭代遍历。如果不线索化,访问了底层节点后就不能再回到上层节点了。
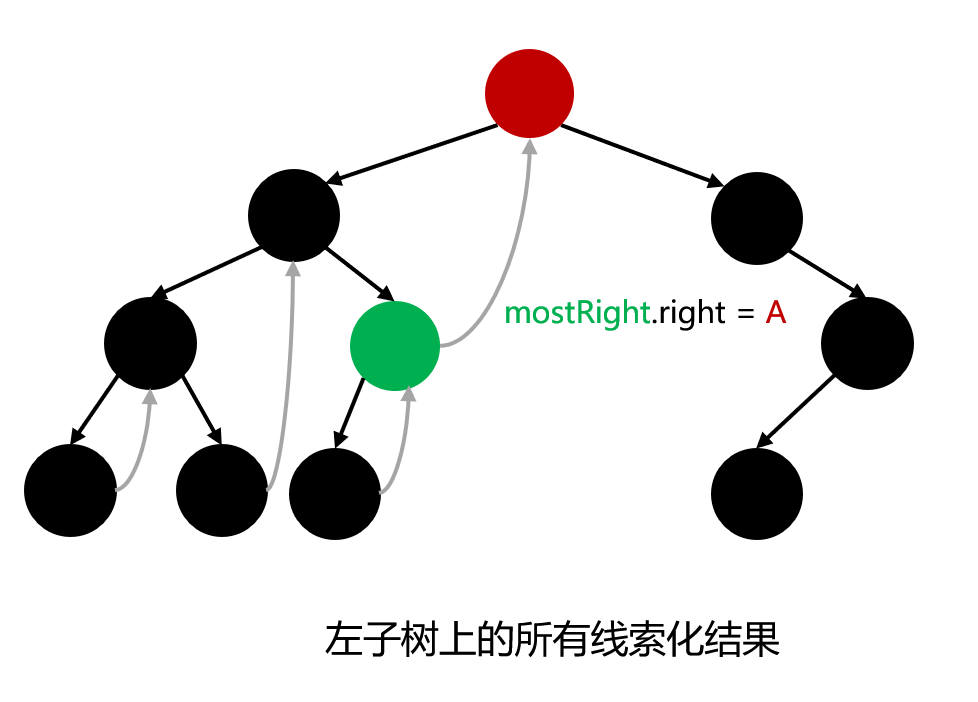
左子树上的线索化结果图示:
没有左孩子的节点只会被遍历一次(因为找不到 mostRight,没有能回溯的线索);有左孩子的节点会被遍历两次(第二次是通过线索回溯到的):
有左孩子,则该节点会被访问两次
第一次访问时,其左子树上的最右节点 的右孩子为 null
第二次访问时,其左子树上的最右节点 的右孩子为该节点
没左孩子,则该节点只会被访问一次
复杂度:
时间复杂度:不同的节点寻找 mostRight 的路径是完全不重合的,因此时间复杂度并没有增加太多,最多是 O(2N),也还是 O(N)。
空间复杂度:O(1)。全局只需要存储 cur 和 mostRight,也没有利用系统栈,不耗费额外空间。
传统递归的方式进行遍历时,是通过系统压栈的方式告诉我们当前节点是第几次被访问,每个节点会被访问三次;但 Morris 遍历并不是,其只能模拟:在左子树上转一圈后回到自身,不能在右子树上转一圈后回到自身(即无法第三次回到自身)。它是利用线索化的机制回到当前节点。
Morris 遍历的特点:可以选择是否要第二次回到当前节点(实现方式为通过当前节点左子树的底层节点的线索化,将right指针指向当前节点来实现)
借助于 Morris 遍历,可以实现出时间复杂度为 O(N),空间复杂度为 O(1) 的前序、中序以及后序遍历。
Morris 遍历代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 public static void morrisTraversal (TreeNode root) if (root == null ) { return ; } TreeNode cur = root; TreeNode mostRight; while (cur != null ) { System.out.print(cur.value + " " ); mostRight = cur.left; if (mostRight != null ) { while (mostRight.right != null && mostRight.right != cur) { mostRight = mostRight.right; } if (mostRight.right == null ) { mostRight.right = cur; cur = cur.left; continue ; } else { mostRight.right = null ; } } cur = cur.right; } System.out.println(" " ); }
注意代码中,第一次和第二次来到节点 A 的时机,这对于修改成前序、中序以及后序遍历来说非常重要。
Morris 版的前序遍历:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 public static void morrisPre (TreeNode root) if (root == null ) { return ; } TreeNode cur = root; TreeNode mostRight; while (cur != null ) { mostRight = cur.left; if (cur.left != null ) { while (mostRight.right != null && mostRight.right != cur) { mostRight = mostRight.right; } if (mostRight.right == null ) { mostRight.right = cur; System.out.print(cur.value + " " ); cur = cur.left; continue ; } else { mostRight.right = null ; } } else { System.out.print(cur.value + " " ); } cur = cur.right; } System.out.println(" " ); }
Morris 版的中序遍历:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public static void morrisIn (TreeNode root) if (root == null ) { return ; } TreeNode cur = root; TreeNode mostRight; while (cur != null ) { mostRight = cur.left; if (mostRight != null ) { while (mostRight.right != null && mostRight.right != cur) { mostRight = mostRight.right; } if (mostRight.right == null ) { mostRight.right = cur; cur = cur.left; continue ; } else { mostRight.right = null ; } } System.out.print(cur.value + " " ); cur = cur.right; } System.out.println(" " ); }
Morris 版的后序遍历:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 public static void morrisPos (TreeNode root) if (root == null ) { return ; } TreeNode cur = root; TreeNode mostRight; while (cur != null ) { mostRight = cur.left; if (mostRight != null ) { while (mostRight.right != null && mostRight.right != cur) { mostRight = mostRight.right; } if (mostRight.right == null ) { mostRight.right = cur; cur = cur.left; continue ; } else { mostRight.right = null ; printEdge(cur.left); } } cur = cur.right; } printEdge(root); System.out.println(" " ); } private static void printEdge (TreeNode cur) if (cur == null ) { return ; } printEdge(cur.right); System.out.println(cur.value); }
直观的理解:每个节点左子树,从右下角向左上角划线逆序打印,整棵树的所有子节点都可以按照这种画法被不漏不重的画出来:
Morris 遍历通常用于以较低的空间复杂度遍历整棵树。
应用一:判断某棵树是否是搜索二叉树
思路:使用 Morris 中序遍历,判断当前值是否大于目前的最大值,若不大于,则不是搜索二叉树。
应用二:恢复搜索二叉树
思路:使用 Morris 中序遍历,判断前一个值 pred 是否大于当前值,若大于,则发现了错误点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public static void printTree (Node head) System.out.println("Binary Tree:" ); printInOrder(head, 0 , "H" , 17 ); System.out.println(); } public static void printInOrder (Node head, int height, String to, int len) if (head == null ) { return ; } printInOrder(head.right, height + 1 , "v" , len); String val = to + head.value + to; int lenM = val.length(); int lenL = (len - lenM) / 2 ; int lenR = len - lenM - lenL; val = getSpace(lenL) + val + getSpace(lenR); System.out.println(getSpace(height * len) + val); printInOrder(head.left, height + 1 , "^" , len); } public static String getSpace (int num) String space = " " ; StringBuffer buf = new StringBuffer("" ); for (int i = 0 ; i < num; i++) { buf.append(space); } return buf.toString(); }
若一棵二叉树根节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值(等于都不行); 它的左、右子树也分别为搜索二叉树。
搜索二叉树(Binary Search Tree)作为一种经典的数据结构,它既有链表的快速插入与删除操作的特点,又有数组快速查找的优势;所以应用十分广泛,例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作。
判断一棵树是否是搜索二叉树有三种方法。
一种简单的方法是首先中序遍历这棵二叉树,并在遍历过程中将每个节点的值保存到一个数组里,遍历完成后,再判断该数组是否是升序的。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public static boolean isSBT01 (Node head) List<Integer> list = new ArrayList<>(); inOrderRecur(head, list); for (int i = 0 ; i < list.size() - 1 ; i++) { if (list.get(i) >= list.get(i+1 )) { return false ; } } return true ; } public static void inOrderRecur (Node head, List<Integer> list) if (head == null ) { return ; } inOrderRecur(head.left, list); list.add(head.value); inOrderRecur(head.right, list); }
方法二需要借助一个静态变量 preMaxValue 存储递归过程中 "当前节点之前的所有节点"的最大值 。因为搜索二叉树是按照中序遍历 的方式升序的,所以当前节点后面的节点值都要大于该最大值 。递归过程中不断保存当前已经遍历过的节点的最大值,并且令后续即将遍历的节点值都要大于该值 。
整个方法栈调用时,是先从左下角的那颗子树开始的,按照 左 -> 头 -> 右 的顺序,依次判断当前节点的值是否大于其左侧的所有节点的最大值 preMaxValue,方法栈不断从左下角开始向右上方向扩展,直到整棵树完成遍历:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public static int preMaxValue = Integer.MIN_VALUE;public static boolean isSBT02 (Node head) if (head == null ) { return true ; } boolean isLeftBst = isSBT02(head.left); if (!isLeftBst) { return false ; } if (preMaxValue >= head.value) { return false ; } else { preMaxValue = head.value; } return isSBT02(head.right); }
与方法二的区别在于使用 Morris 中序遍历节省空间,思路几乎一致。代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public static void morrisIn (TreeNode root) if (root == null ) { return ; } TreeNode cur = root; TreeNode mostRight; while (cur != null ) { mostRight = cur.left; if (mostRight != null ) { while (mostRight.right != null && mostRight.right != cur) { mostRight = mostRight.right; } if (mostRight.right == null ) { mostRight.right = cur; cur = cur.left; continue ; } else { mostRight.right = null ; } } System.out.print(cur.value + " " ); cur = cur.right; } System.out.println(" " ); }
先介绍非标准模板的解法
也可以使用模板套路进行解题,每个节点的左右子树都返回一个 ReturnType 对象,其内即保存了该子树上的最大值和最小值,也保存了该子树是否是搜索二叉树。该对象内保存的最小值是给右子树判断时用,最大值是给左子树判断时用。
方法流程:
遍历到每一个节点时,首先获取左子树的 ReturnData,判断左子树是否满足搜索二叉树:
如果返回值里的 isBST 为 false,说明其左子树不为搜索二叉树
如果当前节点的值小于等于 左子树返回值里的最大值 ,则说明不是搜索二叉树
如果左子树不满足搜索二叉树,则向上返回一个 new ReturnData(false),后续的右子树就不会再去判断了,直接方法栈返回到头结点后返回给主程序 false
如果左子树满足搜索二叉树,则去获取其右子树的 ReturnData,判断右子树是否满足搜索二叉树:
如果返回值里的 isBST为 false,说明其右子树不为搜索二叉树
如果当前节点的值大于等于 右子树返回值里的最小值 ,则说明不是搜索二叉树
如果右子树不满足搜索二叉树,则向上返回一个 new ReturnData(false)
如果左右子树都满足搜索二叉树,则返回一个 ReturnData(leftReturn.min, rightReturn.max),其内保存了当前子树上的最小值和最大值,其中:
当前子树的最小值是左子树上的最小值 当前子树的最大值是右子树上的最大值
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 public static class ReturnData public boolean isSBT = true ; public int min = Integer.MAX_VALUE; public int max = Integer.MIN_VALUE; public ReturnData (boolean isSBT) this .isSBT = isSBT; } public ReturnData (int min, int max) this .min = min; this .max = max; } } public static boolean isSBT03 (Node head) if (head == null ) { return true ; } ReturnData result = checkIsSBT(head); return result.isSBT; } public static ReturnData checkIsSBT (Node head) if (head == null ) { return new ReturnData(true ); } ReturnData leftReturn = checkIsSBT(head.left); if (!leftReturn.isSBT || leftReturn.max >= head.value) { return new ReturnData(false ); } ReturnData rightReturn = checkIsSBT(head.right); if (!rightReturn.isSBT || rightReturn.min <= head.value) { return new ReturnData(false ); } return new ReturnData(leftReturn.min, rightReturn.max); }
注意:上面这种写法并不是标准的模板套路。标准的模板套路是:只在方法的最后进行 return,在方法前面先调用两个递归获取到左右子树上的返回值,据此进行判断后再最后封装成 ReturnData 返回:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public static ReturnData f (Node head) if (head == null ) { return ReturnData(xx, xx, xx); } ReturnData leftReturnData = f(head.left); ReturnData rightReturnData = f(head.right); return new ReturnData(xx, xx, xx); }
在本问题中,使用标准模板的解法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 public static class ReturnData public boolean isSBT = true ; public int min = Integer.MAX_VALUE; public int max = Integer.MIN_VALUE; public ReturnData (boolean isSBT, int min, int max) this .min = min; this .max = max; } } public static boolean isBST04 (Node head) if (head == null ) { return true ; } ReturnData result = checkBST02(head); return result.isSBT; } public static ReturnData checkIsSBT02 (Node head) if (head == null ) { return null ; } ReturnData leftReturn = checkIsSBT02(head.left); ReturnData rightReturn = checkIsSBT02(head.right); boolean isSBT = true ; if (leftReturn != null && (!leftReturn.isSBT || leftReturn.max >= head.value)) isSBT = false ; if (rightReturn != null && (!rightReturn.isSBT || rightReturn.min <= head.value)) isSBT = false ; int min = head.value; int max = head.value; if (leftReturn != null ) { min = Math.min(leftReturn.min, min); max = Math.min(leftReturn.max, max); } if (rightReturn != null ) { min = Math.min(rightReturn.min, min); max = Math.min(rightReturn.max, max); } return new ReturnData(isSBT, min, max); }
这种标准模板的方式存在的缺点:一定会遍历整棵树,因为 return 在方法最后,只会在第三次回到该节点时 return,即只有在遍历过当前节点的左右子树后才会 return,这就导致效率相比上面的方式差了一些(上面的方式是只要在左子树上遇到不满足的子树就直接向上返回到根节点,不会再遍历右子树)
搜索二叉树查找 节点的流程:
如果目标节点值大于当前节点值,则向右递归遍历该树
如果目标节点值小于当前节点值,则向左递归遍历该树
直到找到当前节点的值等于目标节点值 ,即找到了目标节点
搜索二叉树插入 节点的流程:
如果目标节点值大于当前节点值,则向右递归遍历该树
如果目标节点值小于当前节点值,则向左递归遍历该树
直到遍历到底层 时(root == null),即找到了目标节点需要被插入的地方,将其父节点指向目标节点即可(目标节点肯定会被插入到树的某个叶子节点的孩子处 )
搜索二叉树删除 节点的流程:
若目标节点没有左右孩子,说明其是叶子节点,直接将其父节点的对应孩子位置置空 (遍历过程中还需要记录当前节点的父节点,需要在删除了目标节点后将其父节点的对应孩子置空)
若目标节点有左孩子或右孩子(但不同时存在左右孩子),则将其父节点的对应孩子位置设置为目标节点的左或右孩子即可 (让目标节点的孩子代替自己)
若目标节点同时有左孩子和右孩子,则找到其右子树上最左的节点或左子树上最右的节点,令该节点代替自己 ,并且:
若选择右子树的最左节点,则令该节点的父节点的左孩子指向该节点的右子树(令最左节点的右子树代替自己)
若选择左子树的最右节点,则令该节点的父节点的右孩子指向该节点的左子树(令最右节点的左子树代替自己)
一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树 中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树(Complete Binary Tree)。
堆结构即为完全二叉树。
层次遍历常常与队列一起组合出现,因为使用队列先进先出的特点才能保证做到层次遍历,如果是栈结构的先进后出,就无法做到层次遍历
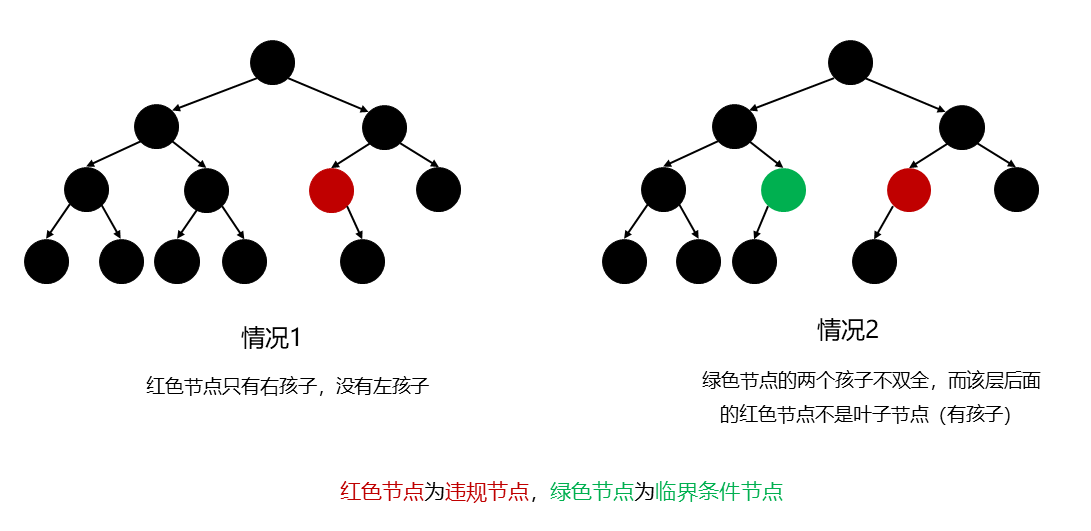
准备一个队列,用于存放层次遍历过程中的每个节点。之所以选择层次遍历,是因为在判断是否满足完全二叉树时有两个判断条件,这两个条件需要依靠层次遍历来实现(因为需要一层一层的遍历,判断当前层内的节点是否满足这两个条件):
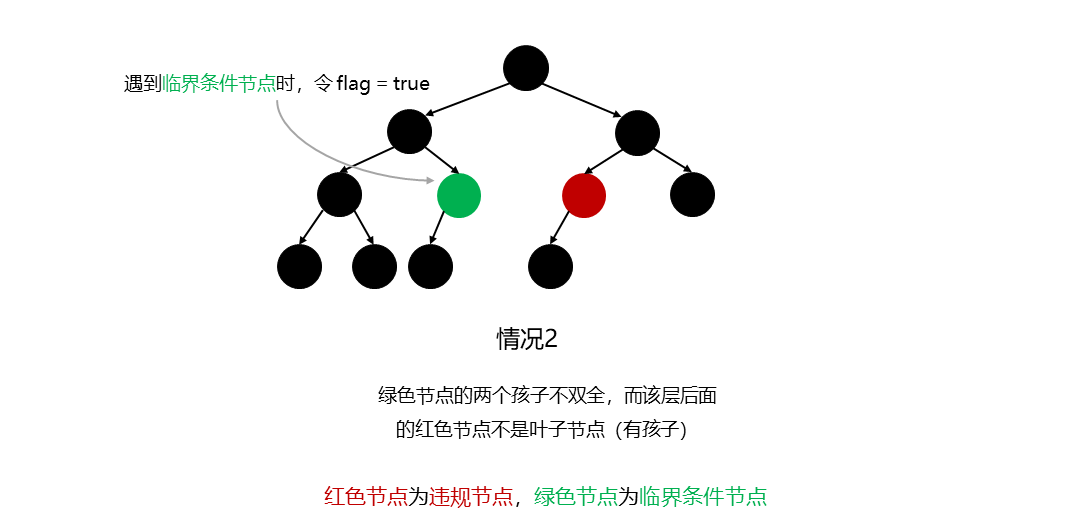
当前节点如果只有右孩子 ,则必定不满足完全二叉树(对应图中情况1)
当前节点如果左右孩子不双全 ,那么当前层所在的后面节点都必须不能有孩子节点 ,即后面的节点都必须是叶子结点 (对应图中情况2)
可以看出,条件2中用到了判断当前层后面节点 是否有孩子节点,所以必须使用层次遍历。
对上述两个条件进行解释:
如果节点如果只有右孩子 ,则根据完全二叉树的定义,其必定不符合,因为完全二叉树里有右孩子的话必定得有左孩子
当前节点如果左右孩子不双全 ,那么说明当前节点为临界条件节点 ,当前层所在的后面节点都必须不能有孩子节点 ,即后面的节点都必须是叶子结点 ,这样才满足完全二叉树的定义
代码实现时:
条件1较好实现,在遍历过程中添加条件判断即可。
条件2的实现则需要借助一个布尔类型的 flag,其在遇到第一个左右孩子不双全 的节点(上图中的绿色)时,将 flag = true,并且在每个节点遍历时,判断 flag 的值,如果为 true,就需要额外判断当前节点是否为叶子结点,如果不是则说明不符合完全二叉树。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 public static boolean isCBT (Node head) if (head == null ) { return true ; } Queue<Node> queue = new LinkedList<>(); queue.add(head); Node left = null ; Node right = null ; boolean flag = false ; while (!queue.isEmpty()) { head = queue.poll(); left = head.left; right = head.right; if ( (left == null && right != null ) || (flag == true && (left != null || right != null ))) { return false ; } if (left != null ) { queue.add(left); } if (right != null ) { queue.add(right); } if (left == null || right == null ) { flag = true ; } } return true ; }
满二叉树(Full Binary Tree):除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树。一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满二叉树。
判断是否是满二叉树的一种方法是使用层次遍历,在遍历的过程中一边记录层数,一边记录节点个数,遍历结束后判断总节点数和层数的关系是否满足满二叉树条件即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 public static boolean isFBT01 (Node head) if (head == null ) { return true ; } Queue<Node> queue = new LinkedList<>(); queue.add(head); Map<Node, Integer> layerMap = new HashMap<>(); layerMap.put(head, 1 ); int curLayer = 0 ; int count = 0 ; while (!queue.isEmpty()) { Node cur = queue.poll(); count++; if (curLayer < layerMap.get(cur)) curLayer++; if (cur.left != null ) { queue.add(cur.left); layerMap.put(cur.left, curLayer + 1 ); } if (cur.right != null ) { queue.add(cur.right); layerMap.put(cur.right, curLayer + 1 ); } } return count == ((1 << curLayer) - 1 ); }
判断满二叉树的模板套路非常简单,只需在向左右孩子索要节点数与层数信息,从而更新自己的节点数与层数信息。递归该过程即可得到整棵树的节点数与层数。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 public static class ReturnData public int nodes; public int layers; public ReturnData (int nodes, int layers) this .nodes = nodes; this .layers = layers; } } public static boolean isFBT02 (Node head) if (head == null ) { return true ; } ReturnData result = checkIsFull(head); return result.nodes == ((1 << result.layers) - 1 ); } public static ReturnData checkIsFull (Node head) if (head == null ) { return new ReturnData(0 , 0 ); } ReturnData leftReturn = checkIsFull(head.left); ReturnData rightReturn = checkIsFull(head.right); int layers = Math.max(leftReturn.layers, rightReturn.layers) + 1 ; int nodes = leftReturn.nodes + rightReturn.nodes + 1 ; return new ReturnData(nodes, layers); }
平衡二叉树(Balanced Binary Tree)又被称为 AVL 树。它具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
使用模板套路即可解该题,定义 ReturnData 记录子树上的节点个数以及是否是平衡二叉树,不断向上返回时判断即可。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 public static class ReturnData public int nodes; public boolean isBBT; public ReturnData (boolean isBBT, int data) this .isBBT = isBBT; this .nodes = data; } } public static boolean isBBT (Node head) if (head == null ) { return true ; } ReturnData result = checkIsBBT(head); return result.isBBT; } public static ReturnData checkIsBBT (Node head) if (head == null ) { return new ReturnData(true , 0 ); } ReturnData leftReturn = checkIsBBT(head.left); ReturnData rightReturn = checkIsBBT(head.right); boolean isBBT = true ; if (!leftReturn.isBBT || !rightReturn.isBBT) isBBT = false ; if (Math.abs(leftReturn.nodes - rightReturn.nodes) > 1 ) isBBT = false ; return new ReturnData(isBBT, Math.max(leftReturn.nodes, rightReturn.nodes) + 1 ); }
不使用模板的剪枝操作:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public boolean isBalanced (TreeNode root) return recur(root) != -1 ; } private int recur (TreeNode root) if (root == null ) return 0 ; int left = recur(root.left); if (left == -1 ) return -1 ; int right = recur(root.right); if (right == -1 ) return -1 ; return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1 ; }
给你一个整数数组 nums ,其中元素已经按升序 排列,请你将其转换为一棵高度平衡 二叉搜索树。高度平衡二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
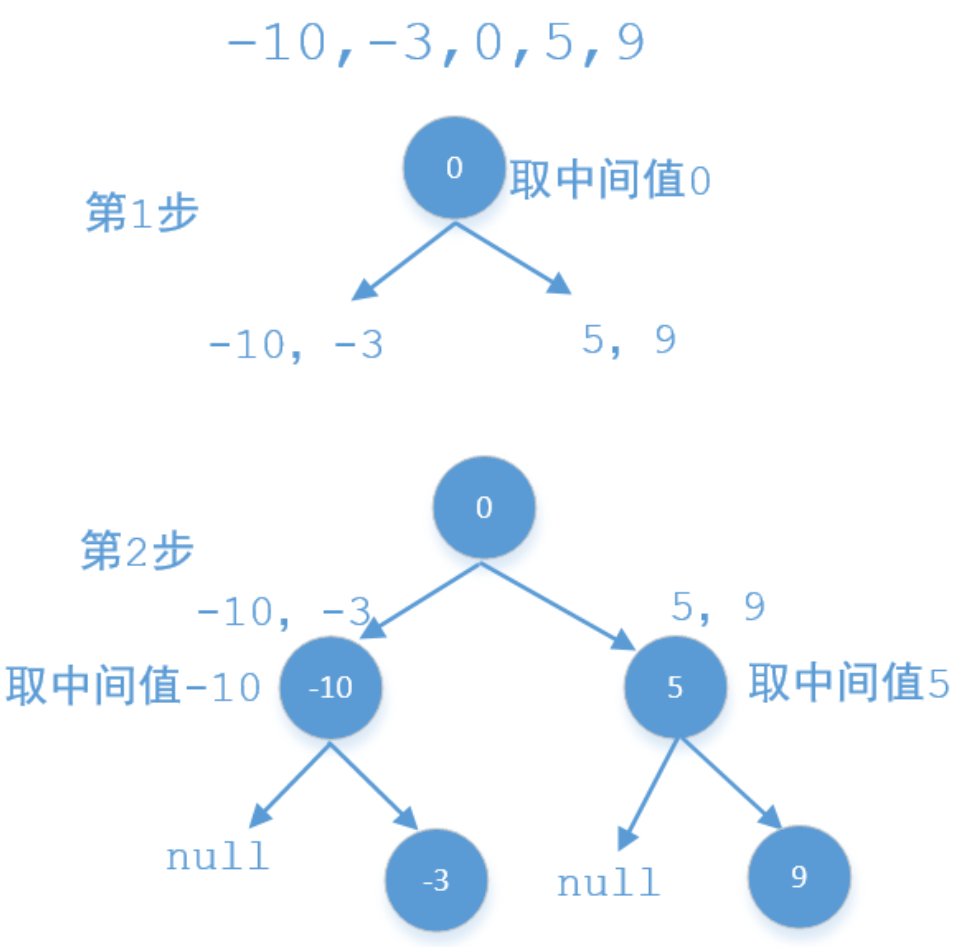
递归解决:使用递归的方式,每次取数组中间的值比如m作为当前节点,m前面的值作为他左子树的结点值,m后面的值作为他右子树的节点值,示例中一个可能的结果是
每次递归时,左子树对应数组 [start, mid - 1],右子树对应数组 [mid + 1, end]。注意是没有取到 mid 的 ,因为 mid 位置的数字已经在当前方法栈中被创建成了一个节点添加到整棵树中,不能将其也放到左右子树的递归里,否则会重复创建节点。
注意边界条件是 start > end。遇到这种情况说明在上一层递归中计算出的 mid 的左侧没有子数组,此时 start == mid,end == mid -1,故其左子树的递归方法里 start > end 。这种情况,说明上一层的 mid 没有了左孩子,因此其左侧递归的结果应该返回 null。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 public TreeNode sortedArrayToBST (int [] nums) return sortedArrayToBSTHelper(nums, 0 , nums.length - 1 ); } public TreeNode sortedArrayToBSTHelper (int [] nums, int start, int end) if (start > end) { return null ; } int mid = (start + end) / 2 ; TreeNode root = new TreeNode(nums[mid]); root.left = sortedArrayToBSTHelper(nums, start, mid - 1 ); root.right = sortedArrayToBSTHelper(nums, mid + 1 , end); return root; }
定义一个 pre 节点,令其不断等于 node 的前一个节点,在第二次回到当前节点时,设置node的前驱为 pre,然后设置 pre 的后继为 node
代码里的两个条件判断不是同时成立的,一个节点只可能某一个成立
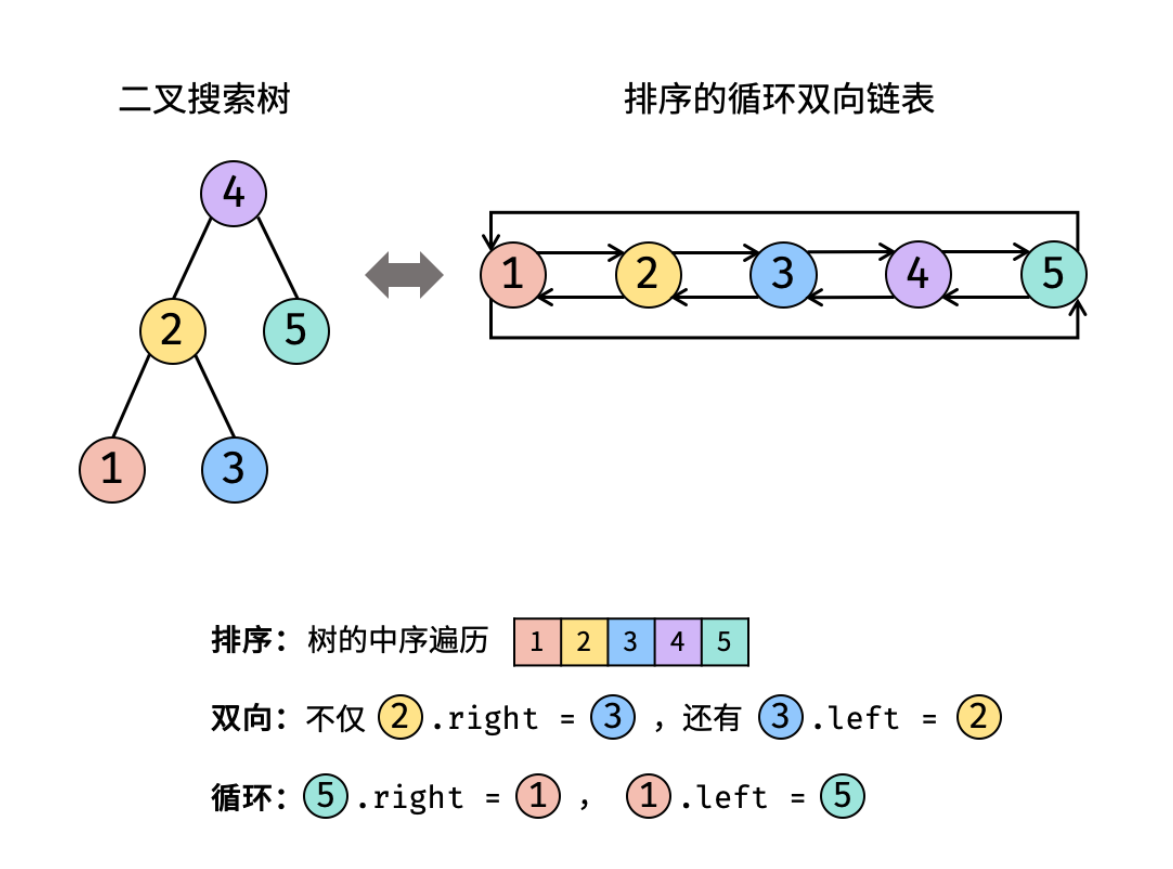
二叉树线索化后,就等于一个双向链表(见书),可以直接按照某种顺序遍历整棵树
自平衡二叉查找树又被称为有序表 ,主要是用它来存储有序的数据
自平衡二叉查找的所有操作的时间复杂度都是 O(logN) 级别。具体实现为:
平衡搜索二叉树(BST)系列
平衡二叉树(AVL树)
节点大小平衡树(Size Balanced Tree)
红黑树(Red–Black Tree)
跳表(Skip List)
四者的时间复杂度相同。
有序表都是搜索二叉树,因此首先介绍搜索二叉树的增删改查操作。
搜索二叉树查找 节点的流程:
如果目标节点值大于当前节点值,则向右递归遍历该树
如果目标节点值小于当前节点值,则向左递归遍历该树
直到找到当前节点的值等于目标节点值 ,即找到了目标节点
搜索二叉树插入 节点的流程:
如果目标节点值大于当前节点值,则向右递归遍历该树
如果目标节点值小于当前节点值,则向左递归遍历该树
直到遍历到底层 时(root == null),即找到了目标节点需要被插入的地方,将其父节点指向目标节点即可(目标节点肯定会被插入到树的某个叶子节点的孩子处 )
搜索二叉树删除 节点的流程:
若目标节点没有左右孩子,说明其是叶子节点,直接将其父节点的对应孩子位置置空 (遍历过程中还需要记录当前节点的父节点,需要在删除了目标节点后将其父节点的对应孩子置空)
若目标节点有左孩子或右孩子(但不同时存在左右孩子),则将其父节点的对应孩子位置设置为目标节点的左或右孩子即可 (让目标节点的孩子代替自己)
若目标节点同时有左孩子和右孩子,则找到其右子树上最左的节点或左子树上最右的节点,令该节点代替自己 ,并且:
若选择右子树的最左节点,则令该节点的父节点的左孩子指向该节点的右子树(令最左节点的右子树代替自己)
若选择左子树的最右节点,则令该节点的父节点的右孩子指向该节点的左子树(令最右节点的左子树代替自己)
https://blog.csdn.net/blueliuyun/article/details/78523937
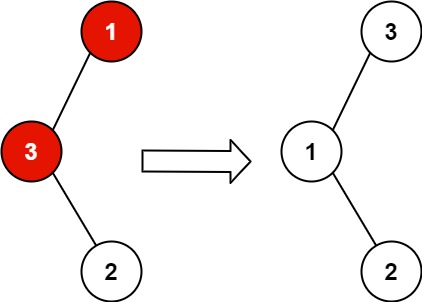
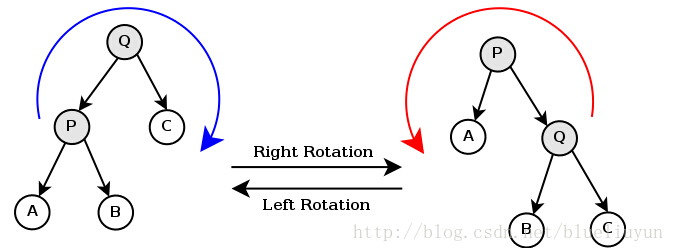
如下图所示的操作被称为对节点Q的右旋 ,对节点P的左旋 。二者互为逆操作。即,右旋——自己变为左孩子的右孩子;左旋——自己变为右孩子的左孩子。
AVL 树需要满足某节点的左右子树的高度差不大于1。
当 AVL 插入一个节点或删除一个节点时,从该节点的父节点开始不断向树的顶部遍历 ,逐个判断当前节点的左右子树是否满足平衡性。如果不满足则开始进行自平衡调整,具体分四种情况:
LR 型:某个节点的左孩子的右子树 subTree 过长。先进行左旋,然后进行右旋,令该右子树 subTree 的根节点成为该子树的根节点
LL 型:某个节点的左孩子 A 的左子树过长。只需要进行一次右旋,令该左孩子 A 成为该子树的根节点
RL 型:某个节点的右孩子的左子树 subTree 过长。先进行右旋,然后进行左旋,令该左子树 subTree 的根节点成为该子树的根节点
RR 型:某个节点的右孩子的右子树过长。只需要进行一次左旋,令该右孩子 A 成为该子树的根节点
更多细节参考文章:https://zhuanlan.zhihu.com/p/56066942
Size Balanced Tree 也是一种自平衡二叉查找树,它的平衡原理是每棵树的大小,不小于其兄弟树的子树的大小 ,即每颗叔叔树的大小,不小于其他任何侄子树的大小。
该树的自平衡操作同样借助于左旋和右旋操作,区别在于:
四种分型的定义区别:例如,LL 型指当前节点的左孩子的左子树的大小,大于当前节点的右子树的大小。LL 型需要将当前节点进行右旋
左右旋的操作和 AVL 树一样
左右旋后,递归判断哪些节点的左右孩子变化了,对左右孩子变化了的节点递归进行该过程,直到令所有节点都符合条件
与 AVL 树一样,当前子树调整完毕后,继续去其父节点上重复该过程直到整棵树完成自平衡
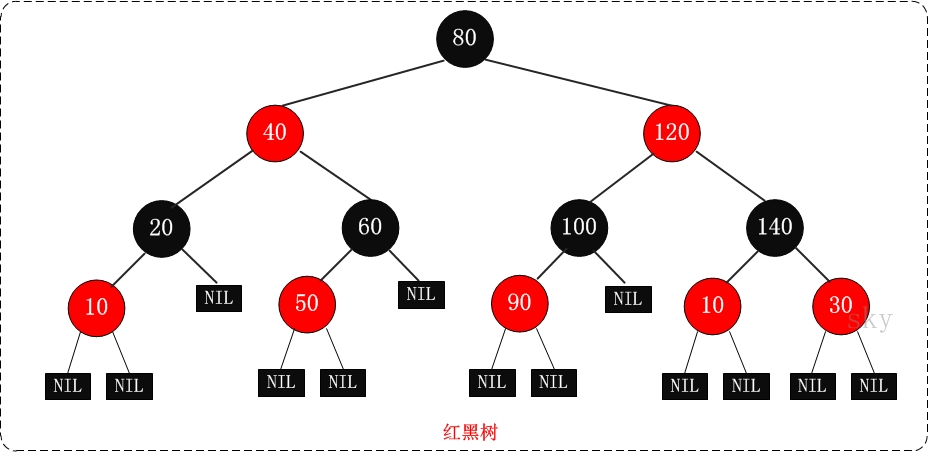
红黑树也是一种自平衡二叉查找树。红黑树的特性:
每个节点或者是黑色,或者是红色
根节点是黑色
每个叶子节点(NIL)是黑色 [注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!]
如果一个节点是红色的,则它的子节点必须是黑色的 (黑色节点却无此要求)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点 (利用该性质实现的平衡性)
剑指 Offer 37. 序列化二叉树
序列化时,进行前序遍历,如果孩子节点不为空就 append 当前节点的 value,中间以 _ 分割,如果为空需要设置为 #(注意这很关键,需要根据 # 判断何时遇到了 null),。序列化示例: 100_21_37_#_#_#_-42_0_#_#_666_#_#_。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 public static String serialByPre (Node head) StringBuilder builder = new StringBuilder(); serializeProcessByPre(head, builder); return builder.toString(); } public static void serializeProcessByPre (Node head, StringBuilder builder) if (head == null ) { builder.append("#_" ); return ; } builder.append(head.value).append("_" ); serializeProcessByPre(head.left, builder); serializeProcessByPre(head.right, builder); }
反序列化时,先将序列化后的字符串 split 拆成字符串数组,然后再进行前序遍历,不断创建节点拼接起来,注意遇到 # 说明当前分支到了底,需要返回 null
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public static Node reconByPreString (String serialString) String[] values = serialString.split("_" ); Queue<String> queue = new LinkedList<>(); for (String value : values) { queue.add(value); } return reconProcess(queue); } public static Node reconProcess (Queue<String> queue) String value = queue.poll(); if (value.equals("#" )) { return null ; } Node node = new Node(Integer.parseInt(value)); node.left = reconProcess(queue); node.right = reconProcess(queue); return node; }
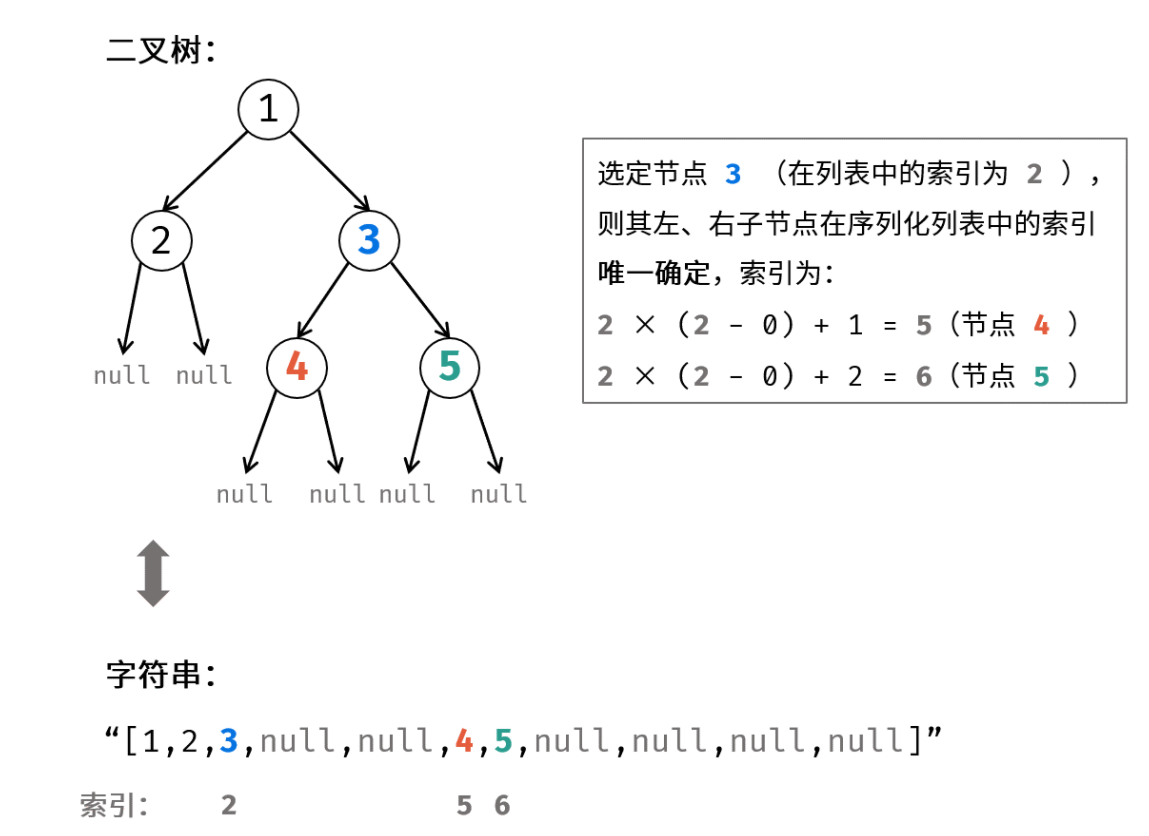
效果:
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 public class Codec public String serialize (TreeNode root) if (root == null ) return "[]" ; StringBuilder res = new StringBuilder("[" ); Queue<TreeNode> queue = new LinkedList<>() {{ add(root); }}; while (!queue.isEmpty()) { TreeNode node = queue.poll(); if (node != null ) { res.append(node.val + "," ); queue.add(node.left); queue.add(node.right); } else res.append("null," ); } res.deleteCharAt(res.length() - 1 ); res.append("]" ); return res.toString(); } public TreeNode deserialize (String data) if (data.equals("[]" )) return null ; String[] vals = data.substring(1 , data.length() - 1 ).split("," ); TreeNode root = new TreeNode(Integer.parseInt(vals[0 ])); Queue<TreeNode> queue = new LinkedList<>() {{ add(root); }}; int i = 1 ; while (!queue.isEmpty()) { TreeNode node = queue.poll(); if (!vals[i].equals("null" )) { node.left = new TreeNode(Integer.parseInt(vals[i])); queue.add(node.left); } i++; if (!vals[i].equals("null" )) { node.right = new TreeNode(Integer.parseInt(vals[i])); queue.add(node.right); } i++; } return root; } }
可以先把两棵树序列化,变成两个字符串,然后 str1.isContain(str2) 直接判断二者是否为包含关系,如果是说明 str2 是 str1 的子树。
1 2 3 4 5 6 7 8 public int maxDepth (Node root) if (root == null ) { return 0 ; } return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1 ; }
第一次遍历到当前节点时,count++;最后一次回到当前节点时,count–;在遇到叶子节点时再更新一次 maxLayer:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public int maxDepth (Node root) if (root == null ) { this .maxLayer = Math.max(this .maxLayer, this .count); return this .maxLayer; } this .count++; maxDepth(root.left); maxDepth(root.right); this .count--; return this .maxLayer; }
使用层次遍历顺序,依次将每一层的节点入队,并且每次遍历一整层的节点,将其左右孩子依次入队,最后再更新一次树的深度。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public int maxDepth (Node root) if (root == null ) { return 0 ; } Queue<Node> queue = new LinkedList<>(); queue.add(root); int maxLayer; while (!queue.isEmpty()) { int size = queue.size(); while (size-- > 0 ) { Node cur = queue.poll(); if (cur.left != null ) queue.add(cur.left); if (cur.right != null ) queue.add(cur.right); } maxLayer++; } return maxLayer; }
可以在层次遍历 的基础上完成该问题的求解。
首先设置几个关键变量:
maxWidth:要求的目标,整棵二叉树的最大宽度。该值将由最大的nextWidth决定nextWidth:当前层的下一层的宽度,将在遍历当前层的孩子节点时不断增大curLayer:当前层的编号,用于判断何时开始换层
并且需要一个HashMap用于存储每一个节点的层编号信息。
方法思路:
首先将根节点入队,并在HashMap中设置其层数编号为1,初始化三个关键参数都为1
弹出队首节点,获取其层数,并与当前层数curLayer对比
若当前层数小于弹出的队首节点,说明该换层了,则将变量进行更新:将下一层宽度nextWidth置空(因为换层后来到的新层还没开始遍历,所以新层的下一层宽度就是0,在后续遍历时才会开始逐渐增加),并更新最大宽度maxWidth
若当前层数等于弹出的队首节点,说明还在当前这一层,不需要做额外操作
遍历当前层,获取当前节点的左右孩子,若存在则放入HashMap中,并保存其孩子的层数编号为curLayer + 1,同时将下一层宽度 nextWidth++,因为当前节点的某一个子孩子被遍历到了,所以下一层宽度加一(在最底层时,因为都没孩子节点了,所以 nextWidth 不会增加,这也符合逻辑)
重复上面步骤,直到队列为空
其中细节:
nextWidth保存的是下一层的节点数,其将在换层时,与 maxWidth 对比,为其赋值因为每次对比的时候,给 maxWidth 赋值的都是下一层的宽度,所以在跳到最后一层的第一个节点时,给 maxWidth 附上了最后一层的信息,所以避免了漏层
每次更新maxWidth的时机都是在换层时,即遍历到下一层的第一个节点时,将原本下一层的宽度值 nextWidth(该值在其上一层遍历左右孩子的时候就已经被更新了,所以这里可以直接获取到,相当于提前更新了下一层的节点数)与当前最大宽度 maxWidth 对比并赋值。
方法思想:层次遍历。提前计算好下一层的最大宽度,在换层时直接提前赋值给 maxWidth ,避免了漏层。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 public static void getTreeMaxWidth (Node head) if (head == null ) { return ; } int maxWidth = 1 ; int nextWidth = 1 ; int curLayer = 1 ; Map<Node, Integer> map = new HashMap<>(); Queue<Node> queue = new LinkedList<>(); queue.add(head); map.put(head, 1 ); while (!queue.isEmpty()) { Node cur = queue.poll(); if (curLayer < map.get(cur)) { maxWidth = Math.max(nextWidth, maxWidth); curLayer++; nextWidth = 0 ; } if (cur.left != null ) { queue.add(cur.left); map.put(cur.left, curLayer+1 ); nextWidth++; } if (cur.right != null ) { queue.add(cur.right); map.put(cur.right, curLayer+1 ); nextWidth++; } } System.out.println("max with = " + maxWidth); }
可以对上述代码进行优化。层次遍历时,可以进行双层 while 循环,外层循环判断当前树的节点是否全部都遍历过,内层循环则负责循环当前层的所有节点 。
具体做法为:在内层 while 循环开始遍历前,首先计算当前队列内的节点个数。这个数字,其实就是目前队列中当前层节点的个数 。
原因:在内层 while 循环里,每次都将当前层的所有节点依次弹出,同时把其左右孩子都入队,这就导致了,第 N 层的 M 个节点都遍历后,队列里就 add 了第 N+1 层的所有节点,这样再进入下一次外层的 while 循环后,再次计算队列里的节点个数时,得到的数量就是第 N+1 层的节点个数。
利用这种思想,可以一次性遍历一整层的节点,从而十分方便地计算当前层宽度
记得当每进入一次外层循环时就令 count = 0,在每一次外层循环即将结束,更新 maxWidth
优化后代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 public static int getTreeMaxWidth3 (Node head) if (head == null ) return 0 ; Queue<Node> queue = new LinkedList<>(); queue.add(head); int maxWidth = 0 ; int count = 0 ; while (!queue.isEmpty()) { count = 0 ; int size = queue.size(); while (size-- > 0 ) { Node cur = queue.poll(); if (cur.left != null ) queue.add(cur.left); if (cur.right != null ) queue.add(cur.right); count++; } maxWidth = Math.max(maxWidth, count); } return maxWidth; }
输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
思路:
先将中序数组里的所有数字及其对应的索引都加入到一个哈希表 中,用于快速查询到前序数组中某个根节点在中序数组中的位置,从而根据该位置将中序数组划分为左右两半
递归方法传入参数:
preRoot:前序 数组中当前子树的根节点的索引值 ,使用该值创建出树结构,并去中序哈希表里查找该根节点在中序数组中的位置
inleft, inright:中序 数组中当前子树的左右边界索引值 ,代表当前子树包含的节点只可能在此区间内
根据传入的 preRoot 创建出对应的树节点,然后利用中序哈希表定位到该节点在中序数组中的位置 i,并据此将中序数组划分为左右两个区间:
中序数组中左子树的范围:[inleft, i - 1]
中序数组中右子树的范围:[i + 1, inright]
根据划分出来的左右子树范围,计算出当前节点的左右子树的根节点(新一轮递归中的根节点)在前序数组中的位置:
preRoot 的左子树的根节点:preRoot + 1
preRoot 的左子树的根节点:preRoot + leftLength + 1 = preRoot + i - inleft + 1
使用计算出的新根节点位置(在前序数组中)以及新根节点的左右边界范围(在中序数组中)进行递归,直到 left > right 时递归返回。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution Map<Integer, Integer> inorderMap; public TreeNode buildTree (int [] preorder, int [] inorder) this .inorderMap = new HashMap<>(); for (int i = 0 ; i < inorder.length; i++) { inorderMap.put(inorder[i], i); } return buildTreeHelper(preorder, 0 , 0 , inorder.length - 1 ); } public TreeNode buildTreeHelper (int [] preorder, int preRoot, int inleft, int inright) if (inleft > inright) { return null ; } TreeNode curRoot = new TreeNode(preorder[preRoot]); int i = this .inorderMap.get(preorder[preRoot]); curRoot.left = buildTreeHelper(preorder, preRoot + 1 , inleft, i - 1 ); int leftLength = i - inleft; curRoot.right = buildTreeHelper(preorder, preRoot + leftLength + 1 , i + 1 , inright); return curRoot; } }
本题给定了两个重要条件:
根据以上条件,可方便地判断 p,q 与 root 的子树关系,即:
若 root.val < p.val,则 p 在 root 右子树 中;
若 root.val > p.val,则 p 在 root 左子树 中;
若 root.val = p.val,则 p 和 root 指向同一节点 。
循环搜索: 当节点 root 为空时跳出;
当 p,q 都在 root 的右子树 中,则遍历至 root.right
否则,当 p,q 都在 root 的左子树 中,则遍历至 root.left
否则,说明找到了最近公共祖先 ,跳出
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public TreeNode lowestCommonAncestor (TreeNode root, TreeNode p, TreeNode q) while (true ) { if (root.val < p.val && root.val < q.val) { root = root.right; } else if (root.val > p.val && root.val > q.val) { root = root.left; } else { break ; } } return root; }
递推工作:
当 p,q 都在 root 的右子树 中,则开启递归 root.right 并返回;
否则,当 p,q 都在 root 的左子树 中,则开启递归 root.left 并返回;
返回值:最近公共祖先 root 。
代码:
1 2 3 4 5 6 7 8 public TreeNode lowestCommonAncestor (TreeNode root, TreeNode p, TreeNode q) if (root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right, p, q); if (root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left, p, q); return root; }
本题是普通的树,而非二叉搜索树,因此不能简单的判断当前节点值是否小于或大于p,q的值。而应该在递归过程中判断当前节点的值是否等于 p 或 q:
如果当前节点为空,则返回 null
若相等,则找到了二者中的某一个,直接向上返回该节点(如果是 p 是 q 的祖先的情况,则此时返回的就是二者中更靠上层的节点,也就是另一个节点的最近祖先)
若不相等,则继续递归向下寻找是够有节点等于 p 或 q
递归方法的返回值共有四种情况:
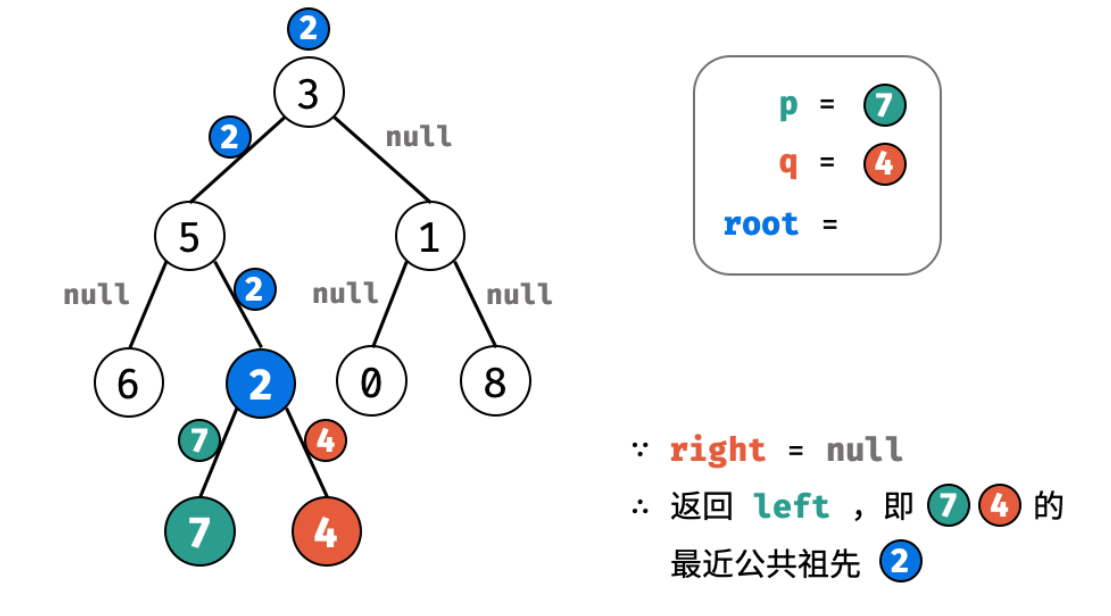
如果 left,right 都为空 ,则当前子树上不包含二者,直接返回 null
如果二者都不为空 ,则当前 root 即为二者的最近公共祖先,返回 root(root 就是左右子树上的 p 和 q 的公共祖先节点)
如果左子树为空 ,右子树不为空 ,则右子树上有 p 或 q(或者都有),左子树上肯定没有 p 和 q,返回 right(right 就是右子树递归向下寻找到的那个等于 p 或 q 的节点,或者是二者的某个祖先节点,该节点被一路向上返回,直到得到答案)
如果右子树为空 ,左子树不为空 ,则左子树上有 p 或 q(或者都有),右子树上肯定没有 p 和 q,返回 left
图解该过程:
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 public TreeNode lowestCommonAncestor (TreeNode root, TreeNode p, TreeNode q) if (root == null || p == null || q == null ) { return null ; } if (p.val == root.val) { return root; } else if (q.val == root.val) { return root; } TreeNode left = lowestCommonAncestor(root.left, p, q); TreeNode right = lowestCommonAncestor(root.right, p, q); if (left == null && right == null ) { return null ; } if (left != null && right != null ) { return root; } if (left == null && right != null ) { return right; } if (right == null && left != null ) { return left; } return null ; }
思路:
第一次遍历二叉树时,使用一个 HashMap 存放每个节点的头节点
然后借助于第一步获取的 HashMap 遍历 o1 的祖先节点们,使用一个 HashSet 存放 o1 节点的祖先节点(注意要包含 o1 自身)
最后遍历 o2 的祖先节点们,判断当前节点是否在第二步创建的 HashSet 里(注意要包含 o2 自身),如果在,说明该节点就是二者的最低公共祖先
需要注意步骤2,3里存储 o1 的祖先节点时需要将 o1 自身也存进去,遍历 o2 的祖先节点时需要将 o2 也进行判断。这是为了在 o1、o2 在同一条链上时不会漏掉 o1 或 o2 自身。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 public static Node lowestCommonAncestor (Node head, Node o1, Node o2) Map<Node, Node> fatherMap = new HashMap<>(); fatherMap.put(head, head); process(head, fatherMap); Set<Node> set1 = new HashSet<>(); Node cur = o1; set1.add(o1); while (cur != fatherMap.get(cur)) { cur = fatherMap.get(cur); set1.add(cur); } cur = o2; while (cur != fatherMap.get(cur)) { if (set1.contains(cur)) return cur; cur = fatherMap.get(cur); } return null ; } public static void process (Node head, Map<Node, Node> fatherMap) if (head == null ) { return ; } if (head.left != null ) fatherMap.put(head.left, head); if (head.right != null ) fatherMap.put(head.right, head); process(head.left, fatherMap); process(head.right, fatherMap); }
简单的想法是在中序遍历的过程中将每个节点保存到一个 List 中,然后再在该 List 里找到其下一个节点即为其后继节点。但是代价是时间复杂度为 O(N),并且空间复杂度也为 O(N)。
如果已知每一个节点的父节点,那么其实目标节点寻找距离自己 K 单位的后继节点所耗费的时间复杂度可以优化到 O(K)。
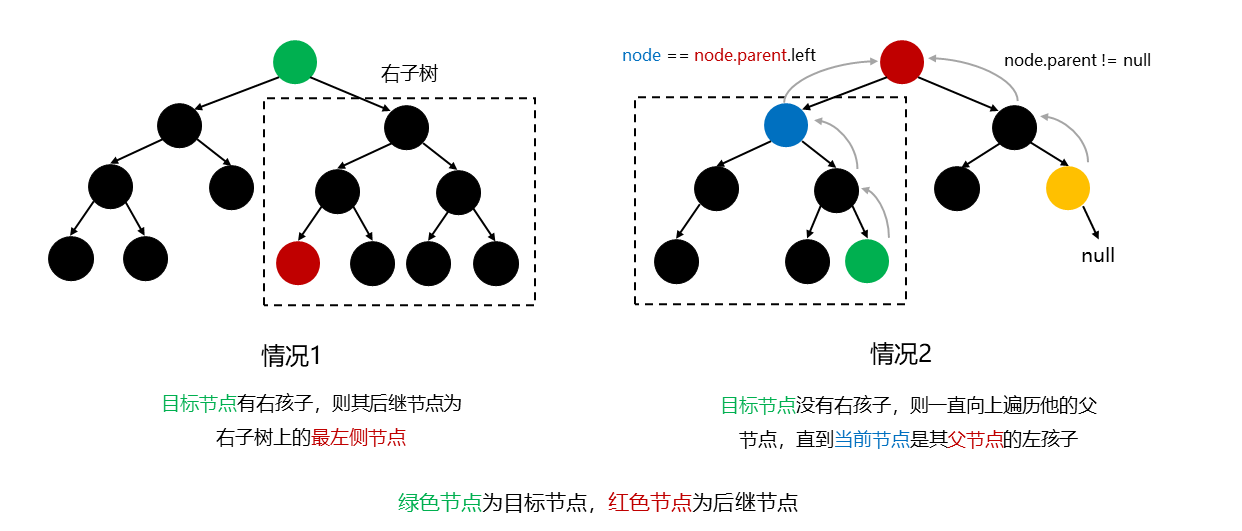
共有三种情况:
目标节点有右孩子:此时目标节点的右孩子所在的右子树上最左边的节点 就是当前节点的后继节点,对应下图中的情况1
目标节点没有右孩子:则一直向上遍历他的父节点,直到当前节点是其父节点的左孩子 ,则这个父节点就是目标节点的后继节点,对应下图中的情况2
目标节点是整棵树最右侧的节点:其后继节点为 null,对应下图中的情况2中的黄色节点
图解:
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 public static Node getSuccessorNode (Node node) if (node == null ) return null ; if (node.right != null ) { return getLeftMostNode(node.right); } while (node.parent != null && node != node.parent.left) { node = node.parent; } return node.parent; } public static Node getLeftMostNode (Node node) if (node == null ) { return null ; } while (node.left != null ) { node = node.left; } return node; }
翻转的本质是:交换每个节点的左右孩子 。
在递归时,不断交换当前节点的左右孩子节点,如此下去,最后就完成了整棵树的翻转。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 public Node invertTree (Node root) if (root == null ) { return null ; } Node tmp = root.right; root.right = root.left; root.left = tmp; invertTree(root.left); invertTree(root.right); return root; }
也可以使用层次遍历。在层次遍历的过程中,先将当前节点的左右孩子进行交换,然后再放入队列中。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public Node invertTree (Node root) if (root==null ) { return null ; } LinkedList<Node> queue = new LinkedList<>(); queue.add(root); while (!queue.isEmpty()) { Node tmp = queue.poll(); Node left = tmp.left; tmp.left = tmp.right; tmp.right = left; if (tmp.left!=null ) { queue.add(tmp.left); } if (tmp.right!=null ) { queue.add(tmp.right); } } return root; }
该方法的空间复杂度会比第一种方法更大。
https://leetcode-cn.com/problems/dui-cheng-de-er-cha-shu-lcof/
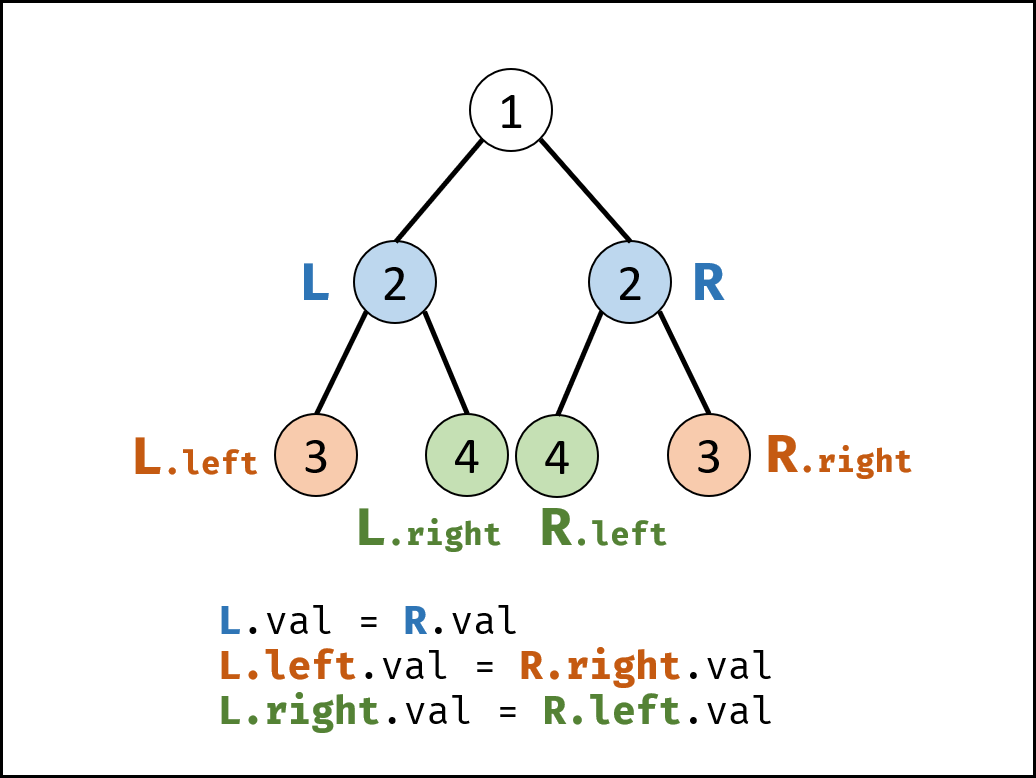
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
思路:递归时每次传入一对节点(这两个节点是位置对称的),例如传入 L.left 和 R.right;另一个递归方法传入 L.right 和 R.left。这样保证每次递归方法里的节点都是位置对称的,因此只需要判断这两个节点的值是否相同即可。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution public boolean isSymmetric (TreeNode root) if (root == null ) { return true ; } return recur(root.left, root.right); } public boolean recur (TreeNode leftSubTree, TreeNode rightSubTree) if (leftSubTree == null || rightSubTree == null ) { return leftSubTree == rightSubTree ? true : false ; } if (leftSubTree.val != rightSubTree.val) { return false ; } return recur(leftSubTree.left, rightSubTree.right) && recur(leftSubTree.right, rightSubTree.left); } }
https://leetcode-cn.com/problems/shu-de-zi-jie-gou-lcof/solution/mian-shi-ti-26-shu-de-zi-jie-gou-xian-xu-bian-li-p/
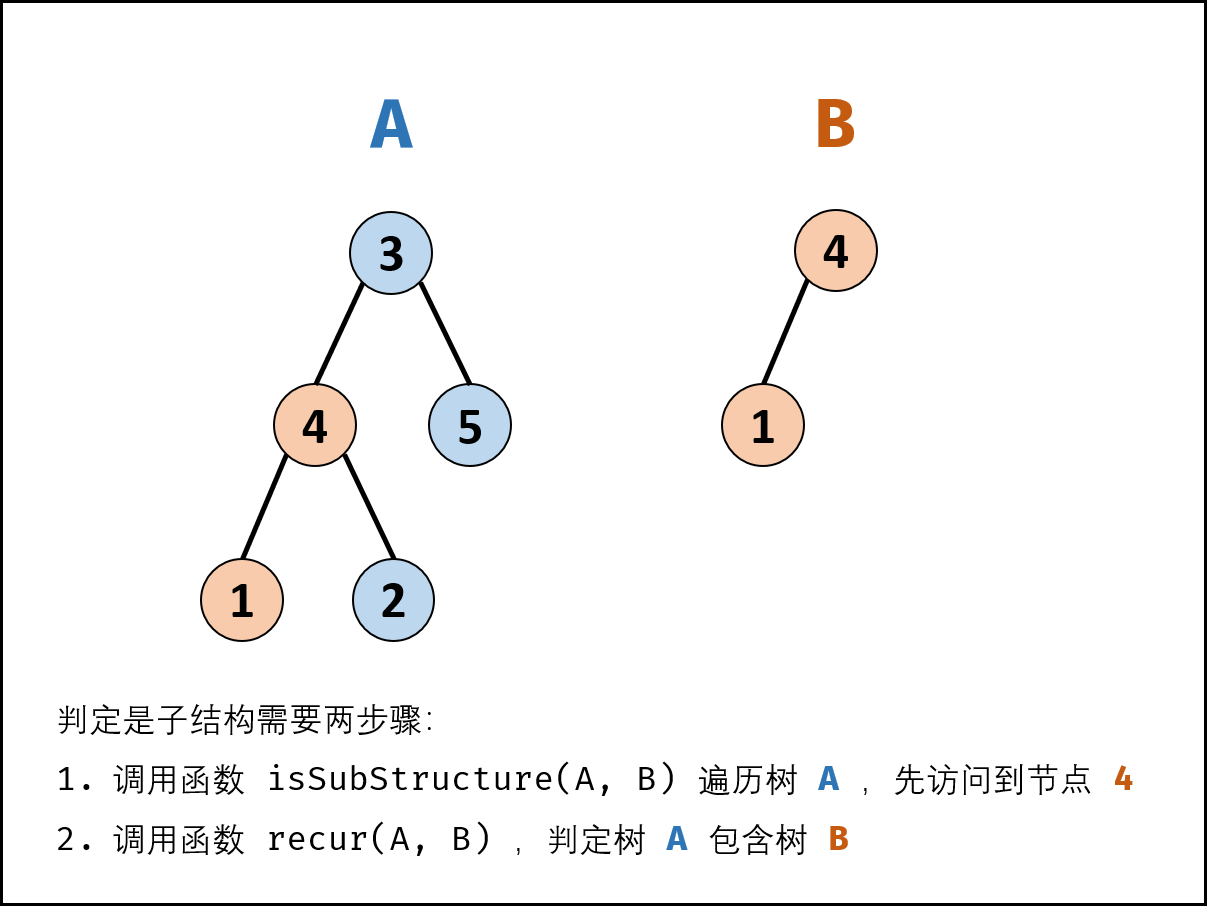
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即A中有出现和B相同的结构和节点值。
思路:双递归,一个递归寻找A中哪个节点与B树的根节点相同;另一个递归在找到相同的节点后开始深入A的当前局部子树进行递归。示意图:
算法流程:
名词规定:树 A*A* 的根节点记作 节点 A*A* ,树 B*B* 的根节点称为 节点 B*B* 。
recur(A, B) 函数:
终止条件:
当节点 B 为空:说明树 B 已匹配完成(越过叶子节点),因此返回 true
当节点 A 为空:说明已经越过树 A 叶子节点,即匹配失败,返回 false
当节点 A 和 B 的值不同:说明匹配失败,返回 false
返回值:
判断 A 和 B 的左子节点是否相等,即 recur(A.left, B.left)
判断 A 和 B 的右子节点是否相等,即 recur(A.right, B.right)
isSubStructure(A, B) 函数:
特例处理: 当 树 A 为空 或 树 B 为空 时,直接返回 false
返回值: 若树 B 是树 A 的子结构,则必满足以下三种情况之一,因此用或 || 连接
以 节点 A 为根节点的子树 包含树 BB ,对应 recur(A, B)
树 B 是 树 A 左子树 的子结构,对应 isSubStructure(A.left, B)
树 B 是 树 A 右子树 的子结构,对应 isSubStructure(A.right, B)
以上 2. 3. 实质上是在对树 AA 做 先序遍历 。
复杂度分析:
时间复杂度 O(MN) : 其中 M,N 分别为树 A 和 树 B 的节点数量;先序遍历树 A 占用 O(M) ,每次调用 recur(A, B)判断占用 O(N) 。
空间复杂度 O(M): 当树 A 和树 B 都退化为链表时,递归调用深度最大。当 M ≤ N 时,遍历树 A 与递归判断的总递归深度为 M ;当 M>N 时,最差情况为遍历至树 A 叶子节点,此时总递归深度为 M。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 public boolean isSubStructure (TreeNode A, TreeNode B) return (A != null && B != null ) && (recur(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B)); } boolean recur (TreeNode A, TreeNode B) if (B == null ) return true ; if (A == null || A.val != B.val) return false ; return recur(A.left, B.left) && recur(A.right, B.right); } public boolean isSubStructure (TreeNode A, TreeNode B) if (A == null || B == null ){ return false ; } boolean res = false ; if (A.val == B.val) { res |= f(A, B); } res |= isSubStructure(A.left, B); res |= isSubStructure(A.right, B); return res; return f(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B); } public boolean f (TreeNode a, TreeNode b) if (a == null ) { return false ; } if (a.val != b.val) { return false ; } boolean res = true ; if (b.left != null ) { res &= f(a.left, b.left); } if (b.right != null ) { res &= f(a.right, b.right); } return res; }
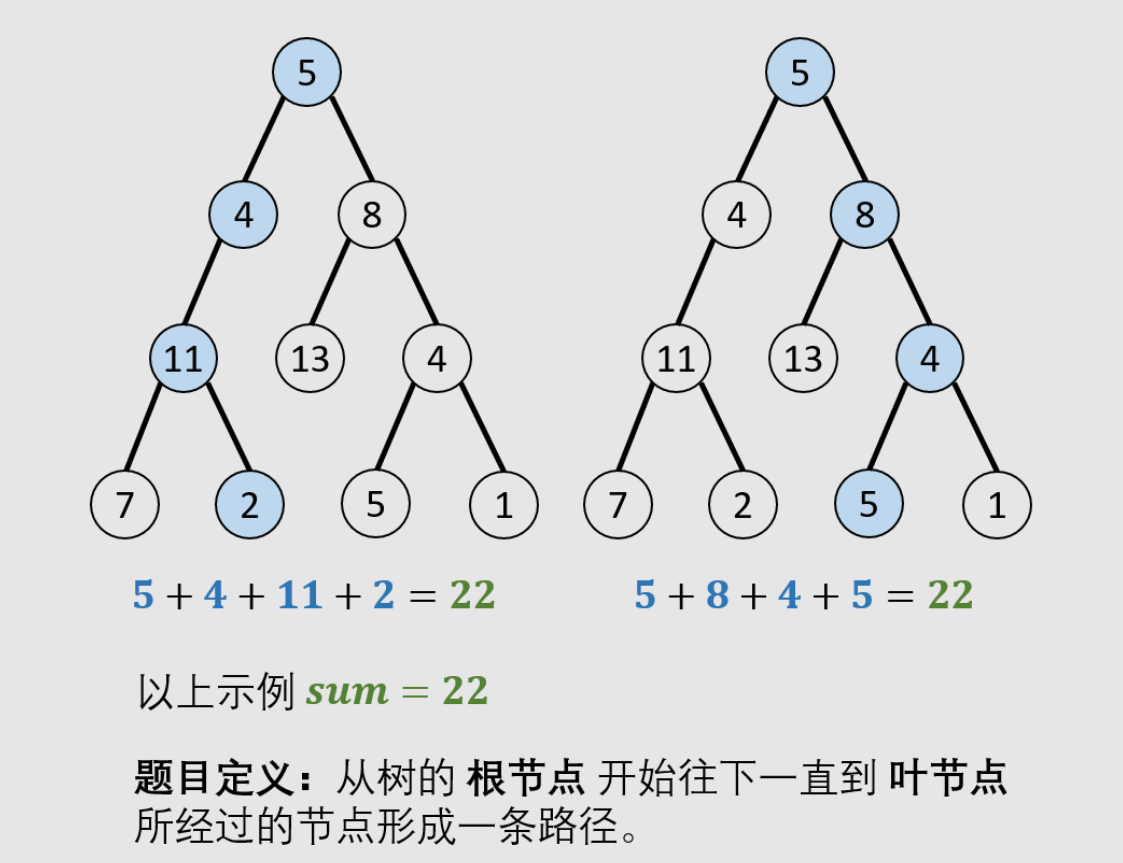
剑指 Offer 34. 二叉树中和为某一值的路径
前序遍历: 按照 “根、左、右” 的顺序,遍历树的所有节点。路径记录: 在先序遍历中,记录从根节点到当前节点的路径。当路径为 ① 根节点到叶节点形成的路径 且 ② 各节点值的和等于目标值 sum 时,将此路径加入结果列表。
注意:记录路径时若直接执行 res.append(path) ,则是将 path 对象加入了 res ;后续 path 改变时, res 中的 path 对象也会随之改变。正确做法:res.append(list(path)) ,相当于复制了一个 path 并加入到 res 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 List<List<Integer>> res = new LinkedList<List<Integer>>(); Deque<Integer> path = new LinkedList<Integer>(); public List<List<Integer>> pathSum(TreeNode root, int target) { dfs(root, target); return ret; } public void dfs (TreeNode root, int target) if (root == null ) { return ; } path.offerLast(root.val); target -= root.val; if (root.left == null && root.right == null && target == 0 ) { res.add(new LinkedList<Integer>(path)); } dfs(root.left, target); dfs(root.right, target); path.pollLast(); }
也可以采用广度优先搜索的方式遍历这棵树。当我们遍历到叶子节点,且此时路径和恰为目标和时,我们就找到了一条满足条件的路径。
为了节省空间,我们使用哈希表记录树中的每一个节点的父节点 。每次找到一个满足条件的节点,我们就从该节点出发不断向父节点迭代 ,即可还原出从根节点到当前节点的路径。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 List<List<Integer>> ret = new LinkedList<List<Integer>>(); Map<TreeNode, TreeNode> map = new HashMap<TreeNode, TreeNode>(); public List<List<Integer>> pathSum(TreeNode root, int target) { if (root == null ) { return ret; } Queue<TreeNode> queueNode = new LinkedList<TreeNode>(); Queue<Integer> queueSum = new LinkedList<Integer>(); queueNode.offer(root); queueSum.offer(0 ); while (!queueNode.isEmpty()) { TreeNode node = queueNode.poll(); int rec = queueSum.poll() + node.val; if (node.left == null && node.right == null ) { if (rec == target) { getPath(node); } } else { if (node.left != null ) { map.put(node.left, node); queueNode.offer(node.left); queueSum.offer(rec); } if (node.right != null ) { map.put(node.right, node); queueNode.offer(node.right); queueSum.offer(rec); } } } return ret; } public void getPath (TreeNode node) List<Integer> temp = new LinkedList<Integer>(); while (node != null ) { temp.add(node.val); node = map.get(node); } Collections.reverse(temp); ret.add(new LinkedList<Integer>(temp)); }
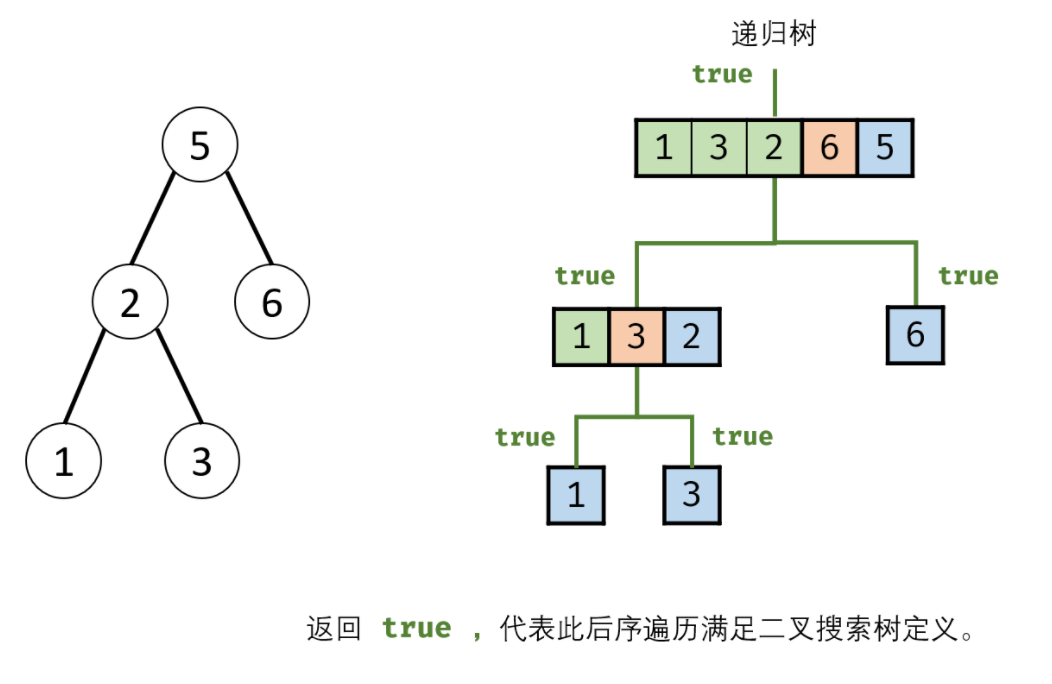
剑指 Offer 33. 二叉搜索树的后序遍历序列 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
解决该问题的关键在于理解后序遍历在数组中的体现:
根节点位置:后序遍历:在数组的最后一个 位置
左右子树的分布特点:后序遍历:左 -> 右 -> 根
因此重点在于如何确定左右子树间的边界 。
一种思路是:根据二叉搜索树的特点,左子树区间内的值都应该小于当前根节点值,右子树区间内的值都应该大于当前根节点值。那么从左往右遍历一遍数组,定位到:第一个大于根节点值的位置 m,则 [left, m - 1] 为左子树区间;[m, right - 1] 为右子树区间。然后继续在右子树区间内遍历,直到与 right 位置相遇。如果无法相遇则代表当前子树不符合;如果可以相遇则代表当前子树符合,那么接着开始递归判断左子树 [left, m - 1] 是否符合,右子树 [m, right - 1] 是否符合。
示意图:
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution public boolean verifyPostorder (int [] postorder) return recur(postorder, 0 , postorder.length - 1 ); } public boolean recur (int [] postorder, int left, int right) if (left >= right) { return true ; } int i = left; while (postorder[i] < postorder[right]) { i++; } int m = i; while (postorder[i] > postorder[right]) { i++; } return i == right && recur(postorder, left, m - 1 ) && recur(postorder, m, right - 1 ); } }
可以尝试倒序重建整棵二叉树,如果重建过程中发现不符合就返回 false。当然不是重建出整棵树的结构,而是判断当前根节点(当前子数组的最后一个节点)是否在合适区间内:
当前根节点的右子树的根节点的值应该大于当前的值且小于最大值
当前根节点的左子树的根节点的值应该小于当前的值且大于最小值
参考的 python 代码:
1 2 3 4 5 6 7 8 9 10 11 12 class Solution : def verifyPostorder (self, postorder: List[int ] ) -> bool: def build (postorder: List[int ], ma: int , mi: int ): if not postorder: return val = postorder[-1 ] if not mi < val < ma: return postorder.pop() build(postorder, ma, val) build(postorder, val, mi) build(postorder, sys.maxsize, -sys.maxsize) return not postorder
117. 填充每个节点的下一个右侧节点指针 II NULL。
思路:一旦在某层的节点之间建立了 next 指针,那这层节点实际上形成了一个链表。因此,如果先去建立某一层的 next 指针,再去遍历这一层,就无需再使用队列了。基于该想法,提出降低空间复杂度的思路:如果第 i 层节点之间已经建立 next 指针,就可以通过 next 指针访问该层的所有节点,同时对于每个第 i 层的节点,我们又可以通过它的 left 和 right 指针知道其第 i+1 层的孩子节点是什么,所以遍历过程中就能够按顺序为第 i + 1 层节点建立 next 指针。
具体来说:
从根节点开始。因为第 0 层只有一个节点,不需要处理。可以在上一层为下一层建立 next 指针。该方法最重要的一点是:位于第 x 层时为第 x + 1 层建立 next 指针。一旦完成这些连接操作,移至第 x + 1 层为第 x + 2 层建立 next 指针。
当遍历到某层节点时,该层节点的 next 指针已经建立。这样就不需要队列从而节省空间。每次只要知道下一层的最左边的节点,就可以从该节点开始,像遍历链表一样遍历该层的所有节点。
在代码实现时,需要设置两重循环:
最外层 while(cur != null) 判断何时遍历完整棵树
内层的 for (; cur != null; cur = cur.next) 判断何时遍历完当前层
在每层遍历完后,更新 cur 为下一层的开始:cur = nextLayerFirstNode
在每一层开始遍历前,都先重置 lastNode = null 以及 nextLayerFirstNode = null
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 class Solution Node lastNode = null ; Node nextLayerFirstNode = null ; public Node connect (Node root) if (root == null ) { return root; } Node cur = root; while (cur != null ) { lastNode = null ; nextLayerFirstNode = null ; for (; cur != null ; cur = cur.next) { if (cur.left != null ) { handle(cur.left); } if (cur.right != null ) { handle(cur.right); } } cur = nextLayerFirstNode; } return root; } public void handle (Node cur) if (lastNode == null ) { nextLayerFirstNode = cur; } else { lastNode.next = cur; } lastNode = cur; } }
剑指 Offer 32 - III. 从上到下打印二叉树 III
有三种方法可以解决该问题:
仍然按照原顺序(从左到右)打印,只不过在每一层保存结果到 list 中时,使用 LinkedList 按照奇偶层选择 addFirst() 还是 addLast() 添加到 当前层的 tmp 链表里。该方法无法实现真正的之字形打印,只是保证了答案链表里的顺序
使用双端队列,每次遍历连续的奇、偶两层:
在奇数层:removeFirst() 获取当前节点。addLast() 先左孩子再右孩子
在偶数层:removeLast() 获取当前节点。addFirst() 先右孩子再左孩子
使用两个栈,一个栈存储奇数层的,一个栈存储偶数层的
遍历奇数层时,向偶数栈中压入当前层的孩子;先左后右
遍历偶数层时,向奇数栈中压入当前层的孩子;先右后左
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 public List<List<Integer>> levelOrder(TreeNode root) { if (root == null ) { return new ArrayList<>(); } List<List<Integer>> ans = new ArrayList<>(); Queue<TreeNode> queue = new LinkedList<>(); queue.add(root); TreeNode cur = null ; while (!queue.isEmpty()) { int size = queue.size(); LinkedList<Integer> tmp = new LinkedList<>(); while (size-- > 0 ) { cur = queue.poll(); if (ans.size() % 2 == 0 ) { tmp.addLast(cur.val); } else { tmp.addFirst(cur.val); } if (cur.left != null ) { queue.add(cur.left); } if (cur.right != null ) { queue.add(cur.right); } } ans.add(tmp); } return ans; } public List<List<Integer>> levelOrderDeque(TreeNode root) { Deque<TreeNode> queue = new LinkedList<>(); List<List<Integer>> res = new ArrayList<>(); queue.addFirst(root); while (!queue.isEmpty()) { int size = queue.size(); List<Integer> list = new ArrayList<>(); while (size-- > 0 ) { root = queue.removeFirst(); list.add(root.val); if (root.left != null ) { queue.addLast(root.left); } if (root.right != null ) { queue.addLast(root.right); } } res.add(list); if (!queue.isEmpty()) { size = queue.size(); list = new ArrayList<>(); while (size-- > 0 ) { root = queue.removeLast(); list.add(root.val); if (root.right != null ) { queue.addFirst(root.right); } if (root.left != null ) { queue.addFirst(root.left); } } res.add(list); } } return res; } public List<List<Integer>> levelOrderTwoStack(TreeNode root) { List<List<Integer>> res = new ArrayList<>(); Stack<TreeNode> stackOdd = new Stack<>(); Stack<TreeNode> stackEven = new Stack<>(); stackOdd.push(root); while (!stackOdd.isEmpty() || !stackEven.isEmpty()) { List<Integer> list = new ArrayList<>(); if (!stackOdd.isEmpty()) { while (!stackOdd.isEmpty()) { root = stackOdd.pop(); list.add(root.val); if (root.left != null ) { stackEven.push(root.left); } if (root.right != null ) { stackEven.push(root.right); } } } else { while (!stackEven.isEmpty()) { root = stackEven.pop(); list.add(root.val); if (root.right != null ) { stackOdd.push(root.right); } if (root.left != null ) { stackOdd.push(root.left); } } } res.add(list); } return res; }
许多二叉树问题都可以使用中序遍历 + pre 变量的套路解决。在中序遍历的过程中,使用 pre 变量不断记录当前节点的前一个节点,从而解决问题。其中中序遍历的实现既可以使用递归栈又可以使用 Morris 遍历。
模板一:递归
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public Node pre;public void template01 (Node root) if (root == null ) { return null ; } dfs(root); } void dfs (Node cur) if (cur == null ) { return ; } dfs(cur.left); if (pre != null ) { } else { pre = cur; } dfs(cur.right); }
模板二:Morris 遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 public Node template (Node root) if (root == null ) { return null ; } Node cur = root; Node mostRight = null ; Node pre = null ; Node head = null ; while (cur != null ) { mostRight = cur.left; if (mostRight != null ) { while (mostRight.right != null && mostRight.right != cur) { mostRight = mostRight.right; } if (mostRight.right == null ) { mostRight.right = cur; cur = cur.left; continue ; } if (mostRight.right == cur) { mostRight.right = null ; } } if (pre != null ) { pre = cur; } else { pre = cur; } cur = cur.right; } return head; }
剑指 Offer 36. 二叉搜索树与双向链表
在
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 public Node pre, head;public Node treeToDoublyList01 (Node root) if (root == null ) return null ; dfs(root); head.left = pre; pre.right = head; return head; } void dfs (Node cur) if (cur == null ) return ; dfs(cur.left); if (pre != null ) pre.right = cur; else head = cur; cur.left = pre; pre = cur; dfs(cur.right); }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 public Node treeToDoublyList02 (Node root) if (root == null ) { return null ; } Node cur = root; Node mostRight = null ; Node pre = null ; Node head = null ; while (cur != null ) { mostRight = cur.left; if (mostRight != null ) { while (mostRight.right != null && mostRight.right != cur) { mostRight = mostRight.right; } if (mostRight.right == null ) { mostRight.right = cur; cur = cur.left; continue ; } if (mostRight.right == cur) { mostRight.right = null ; } } if (pre != null ) { pre.right = cur; cur.left = pre; pre = cur; } else { pre = cur; head = cur; } cur = cur.right; } pre.right = head; head.left = pre; return head; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 public class ReturnData public Node mostLeft; public Node mostRight; public ReturnData (Node left, Node right) this .mostLeft = left; this .mostRight = right; } } public Node treeToDoublyList01 (Node root) if (root == null ) { return null ; } globalRoot = root; head = root; recur(root); return head; } public Node globalRoot;public Node head;public ReturnData recur (Node root) if (root == null ) { return new ReturnData(null , null ); } ReturnData leftReturn = recur(root.left); ReturnData rightReturn = recur(root.right); Node curMostLeft = leftReturn.mostLeft; Node curMostRight = rightReturn.mostRight; if (leftReturn.mostRight != null ) { leftReturn.mostRight.right = root; root.left = leftReturn.mostRight; } if (rightReturn.mostLeft != null ) { rightReturn.mostLeft.left = root; root.right = rightReturn.mostLeft; } if (leftReturn.mostLeft == null ) { curMostLeft = root; } if (rightReturn.mostRight == null ) { curMostRight = root; } if (root == globalRoot) { head = curMostLeft; curMostLeft.left = curMostRight; curMostRight.right = curMostLeft; } return new ReturnData(curMostLeft, curMostRight); }
给你二叉搜索树的根节点 root ,该树中的两个节点被错误地交换。请在不改变其结构的情况下,恢复这棵树。示例:
这道题的关键在于正确的分析错误的两个点的位置。例如 [1, 2, 3, 4, 5, 6, 7] 被交换成了 [1, 6, 3, 4, 5, 2, 7],当中序遍历时,不断判断当前 i 是否大于 i+1
如果是,则记录 i 是那个较大的错误点,即 index2,i+1 不是错误点(这点不能乱,错误的是 i,不是i+1)。
当再次发现 i > i+1 时,即 5 > 2,此时错误的就不是 i 了,而是 i+1,这个点就是 index1 。
最后交换 index1 和 index2
具体实现:只需要在中序遍历的时候不断记录 pred 点(i),比较当前点(i+1)的值。如果pred更大,说明他就是 index2。再找下去,pred 再次大于 cur 时,cur 就是 index1。最后做交换即可
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 class Solution public TreeNode errorRoot; public TreeNode errorcChild; public TreeNode pred; public TreeNode node01; public TreeNode node02; public int count = 2 ; public void recoverTree (TreeNode root) if (root == null ) return ; inOrderRecur(root); int tmp = node01.val; node01.val = node02.val; node02.val = tmp; } public void inOrderRecur (TreeNode cur) if (cur == null ) { return ; } inOrderRecur(cur.left); if (pred != null && pred.val > cur.val) { if (--count == 0 ) { node02 = cur; } else { node01 = pred; node02 = cur; } } pred = cur; inOrderRecur(cur.right); } }
对于这种跟中序遍历相关的题目,可以考虑使用 Morris 中序遍历降低空间复杂度。思路同样是在中序遍历的过程中,比较 pred 与 cur 的大小。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 public void recoverTree (TreeNode root) if (root == null ) { return ; } TreeNode cur = root; TreeNode mostRight; TreeNode x = null ; TreeNode y = null ; TreeNode pred = null ; while (cur != null ) { mostRight = cur.left; if (mostRight != null ) { while (mostRight.right != null && mostRight.right != cur) { mostRight = mostRight.right; } if (mostRight.right == null ) { mostRight.right = cur; cur = cur.left; continue ; } else { mostRight.right = null ; } } if (pred != null && pred.val > cur.val) { x = cur; if (y == null ) { y = pred; } } pred = cur; cur = cur.right; } int tmp = x.val; x.val = y.val; y.val = tmp; }
剑指 Offer 54. 二叉搜索树的第k大节点 k 大的节点的值。
思路:
维护一个小根堆,只保存 k 个节点的值,中序遍历完毕后堆顶就是第 k 大的节点值
倒序中序遍历,k–,效率最高
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 public int kthLargest (TreeNode root, int k) if (root == null || k < 1 ) { return 0 ; } Queue<Integer> heap = new PriorityQueue<>(); recur(root, heap, k); return heap.poll(); } public void recur (TreeNode root, Queue<Integer> heap, int k) if (root == null ) { return ; } recur(root.left, heap, k); if (heap.size() < k) { heap.offer(root.val); } else { heap.poll(); heap.offer(root.val); } recur(root.right, heap, k); } public int kthLargest (TreeNode root, int k) if (root == null ) { return -1 ; } this .K = k; recur(root); return ans; } public int K;public int ans;public void recur (TreeNode root) if (root == null ) { return ; } recur(root.right); if (--this .K == 0 ) { this .ans = root.val; return ; } recur(root.left); }
符合模板套路的特点:可以通过当前节点向左右子树索要一些信息(例如节点数,层数等),从而递归地解决问题。
模板:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public static ReturnData f (Node head) if (head == null ) { return ReturnData(xx, xx, xx); } ReturnData leftReturnData = f(head.left); ReturnData rightReturnData = f(head.right); return new ReturnData(xx, xx, xx); }
一些问题需要在当前子树上进行分类:考虑当前节点 或不考虑当前节点 两种情况,分别计算两种情况中的最优解,进行返回。
从二叉树的节点a出发,可以向上或者向下走,但沿途的节点只能经过一次,到达节点b时路径上的节点个数叫作a到b的距离,那么二叉树任何两个节点之间都有距离,求整棵树上的最大距离。
当前子树的最大距离分两种情况:
考虑当前节点时:最大距离为左子树的高度 + 右子树高度 + 1
不考虑当前节点时:最大距离为左子树上的最大距离或右子树上的最大距离
最后返回二者中的最大值。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 public class MaxDistance public static class TreeNode public int value; TreeNode left; TreeNode right; public TreeNode (int data) this .value = data; } } public static class ReturnData int height; int maxLength; public ReturnData (int height, int count) this .height = height; this .maxLength = count; } } public static int maxDistance (TreeNode root) ReturnData res = process(root); return res.maxLength; } public static ReturnData process (TreeNode root) if (root == null ) { return new ReturnData(0 , 0 ); } ReturnData leftReturn = process(root.left); ReturnData rightReturn = process(root.right); int curHeight = Math.max(leftReturn.height, rightReturn.height) + 1 ; int length1 = leftReturn.height + rightReturn.height + 1 ; int length2 = Math.max(leftReturn.maxLength, rightReturn.maxLength); return new ReturnData(curHeight, Math.max(length1, length2)); } }
情况:
当前员工要来——其直接下级不能来
当前员工不来——其直接下级可以选择:来或不来
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 import java.util.List;public class MaxHappyValue public static class Employee public int happy; List<Employee> subordinates; } public static class ReturnData int happyValue; public ReturnData (int v) this .happyValue = v; } } public static int maxHappyValue (Employee boss) return Math.max(recur(boss, true ), recur(boss, false )); } public static int recur (Employee cur, boolean consider) if (cur.subordinates == null ) { return consider ? cur.happy : 0 ; } int p1 = 0 ; int p2 = 0 ; if (consider) { p1 += cur.happy; for (Employee subordinate : cur.subordinates) { p1 += recur(subordinate, false ); } } else { for (Employee subordinate : cur.subordinates) { p2 += recur(subordinate, true ); } } return Math.max(p1, p2); } public static int maxHappy (int [][] matrix) int [][] dp = new int [matrix.length][2 ]; boolean [] visited = new boolean [matrix.length]; int root = 0 ; for (int i = 0 ; i < matrix.length; i++) { if (i == matrix[i][0 ]) { root = i; } } process(matrix, dp, visited, root); return Math.max(dp[root][0 ], dp[root][1 ]); } public static void process (int [][] matrix, int [][] dp, boolean [] visited, int root) visited[root] = true ; dp[root][1 ] = matrix[root][1 ]; for (int i = 0 ; i < matrix.length; i++) { if (matrix[i][0 ] == root && !visited[i]) { process(matrix, dp, visited, i); dp[root][1 ] += dp[i][0 ]; dp[root][0 ] += Math.max(dp[i][1 ], dp[i][0 ]); } } } public static void main (String[] args) int [][] matrix = { { 1 , 8 }, { 1 , 9 }, { 1 , 10 } }; System.out.println(maxHappy(matrix)); } }
给定一个非负整数n,代表二叉树的节点个数。返回能形成多少种不同的二叉树结构。
思路:当前位置作为根节点时,左子树的节点个数从 0 开始遍历一直到 n - 1,累加各种情况下当前子树的结构种类:
1 2 res += process(i, record) * process(n - 1 - i, record);
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 public class NumberOfTree public static int numberOfTree (int n) int [] record = new int [n + 1 ]; return process(n, record); } private static int process (int n, int [] record) if (n < 0 ) { return 0 ; } if (n == 0 ) { return 1 ; } if (n == 1 ) { return 1 ; } if (n == 2 ) { return 2 ; } if (record[n] != 0 ) { return record[n]; } int res = 1 ; for (int i = 0 ; i <= n - 1 ; i++) { res += process(i, record) * process(n - 1 - i, record); } return res; } public static void main (String[] args) System.out.println(numberOfTree(4 )); } }