【算法】二分查找法

发表于2021-11-24更新于2022-02-22字数统计7k阅读时长51分阅读次数

二分查找法模板

https://leetcode-cn.com/leetbook/read/binary-search/x6q6fi/

模板一

二分查找法的标准模板适用于只需要寻找某一个符合条件的值：

  • 初始化 right = nums.length - 1
  • 更新区间时：left = mid + 1；right = mid - 1
  • 查找的区间为 [left, right]，左闭右闭
  • 跳出 while 循环的条件是 left == right + 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public int binarySearch(int[] nums, int target) {
    if(nums == null || nums.length == 0)
        return -1;

    int left = 0;
    int right = nums.length - 1;
    int mid;

    while (left <= right) {
        mid = left + (right - left >> 1);
        if (nums[mid] == target) {
            // 只要找到一个目标值即可返回
            return mid;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] < target) {
            left = mid + 1;
        }
    }
    // left == right + 1，如果到这里还没找到说明整个数组里没有任何一个满足条件的元素，返回-1
    return -1;
}

模板二

二分查找法的标准模板适用于寻找符合条件的最左边界：

  • 初始化 right = nums.length
  • 更新区间时：left = mid + 1；right = mid
  • 查找的区间为 [left, right)，左闭右开
  • 跳出 while 循环的条件是 left == right

之所以更新右指针为 right = mid：

  • 一是因为要求解最左边界，则在 right 更新时需要保存着当前满足条件的值（该值左侧可能还有满足条件的值，需要用 right 保存着当前满足的值），最后跳出循环时其位置就是最左满足条件的值
  • 二是因为查找区间为左闭右开，不包含 right。因此在发现 mid 位置满足条件时，接下来的二分过程中，要令 right = mid，这样 mid 因为右开而不被考虑，mid - 1 能正常被考虑。否则若 right = mid - 1，则下一轮的二分中 mid - 1 就没有被考虑在内，从而漏算了该值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public int binarySearch(int[] nums, int target) {
    if(nums == null || nums.length == 0)
        return -1;

    int left = 0;
    int right = nums.length;
    int mid;

    while (left < right) {
        mid = left + (right - left >> 1);
        if (nums[mid] >= target) {
            // 要寻找满足条件的最左区间，因此满足条件也不能退出，而是继续更新右边界
            // 右边界要保存着当前满足条件的值
            right = mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        }
    }
    // 退出循环时，left == right，需要额外判断一下left位置的元素值是否满足条件
    return nums[left] == target ? left : -1;
}

许多求解最左/由边界的题目其实都可以使用模板一，只需要额外借助一个变量 ans，在二分过程中记录下满足条件的值（不要 return），然后继续二分直到跳出循环，这样到最后 ans 就保存了最左/右边界

模板二适合于在遍历过程中，mid 位置很可能就是符合题意的答案，但是因为在二分过程中没有写“遇到答案立即返回”的代码，因此需要考虑到 mid 就是答案的情况，在 right 更新时要包含 mid，不能将其跳过。

关于二分查找法模板的更多细节：https://blog.csdn.net/xiao_jj_jj/article/details/106018702

二分查找法常见题目

可以使用二分法的题目的一个特点：单调性

搜索旋转排序数组

https://leetcode-cn.com/problems/search-in-rotated-sorted-array/solution/sou-suo-xuan-zhuan-pai-xu-shu-zu-by-leetcode-solut/

整数数组 nums 按升序排列，数组中的值互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你旋转后的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

img

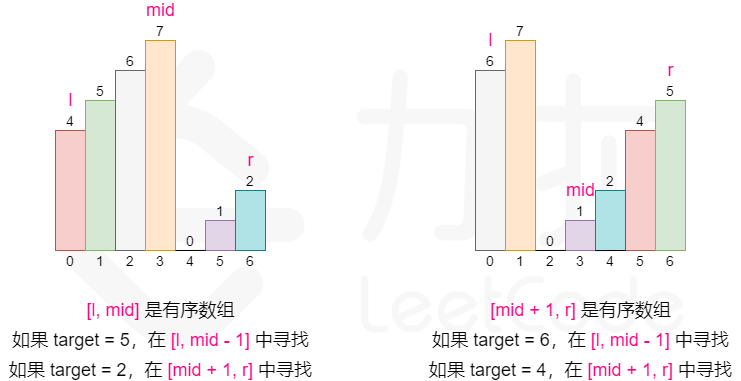
思路：这道题的关键是找到单调性。

最关键的一步就是通过 nums[mid] 和 nums[0] 的大小差别，判断 mid 左侧还是右侧是有序数组（也就是找单调性）。 我们只在有序数组里判断 target 是否在其内，不在其中，那肯定在另一侧无序数组里
通过这点来进行二分查找。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
    public int search(int[] nums, int target) {
        if (nums == null || nums.length < 1) {
            return -1;
        }
        int left = 0;
        int right = nums.length - 1;
        int mid;

        // 在有序的区间范围内判断 target 是否在该区间内
        // 在该区间内的话，就可以继续二分，缩小区间，

        // 最关键的一步就是通过 nums[mid] 和 nums[0] 的大小差别，判断 mid 左侧还是右侧是有序数组（也就是找单调性）
        // 我们只在有序数组里判断 target 是否在其内，不在其中，那肯定在另一侧无序数组里
        // 通过这点来进行二分查找
        while (left <= right) {
            mid = left + (right - left >> 1);
            if (nums[mid] == target) {
                return mid;
            } 
            // 判断mid的左侧是有序数组还是右侧是有序数组
            // 注意带上 等于号
            if (nums[0] <= nums[mid]) {
               // 如果左侧是有序数组，则判断一下 target 的大小是否处于该区间内
               // 注意有等于号
               // 因为 target 肯定不等于 nums[mid] 了，否则上面就返回了
               if (target >= nums[left] && target < nums[mid]) {
                   // 如果处于该区间内，则直接忽略掉另一侧不是有序的数组，在当前数组里继续二分查找，因为 target 肯定不在另一个数组里
                   // 此时就可以更新 right 为 mid-1，肯定在[left,mid-1]区间内
                   right = mid - 1;
               } else {
                   left = mid + 1;
               }
            } else {
                // 如果左侧不是有序的，那么右侧就是有序的了
                // 如果 target 在右侧的数组中，则缩小查找范围为 [mid+1, right]
                // 注意有等于号
                if (target > nums[mid] && target <= nums[right]) {
                    left = mid + 1;
                } else {
                    // 如果在左侧数组（无序的部分），则缩小查找范围为 [left, mid-1]
                    right = mid - 1;
                }
            }
        }
        return -1;
    }
}

旋转数组的最小数字

https://leetcode-cn.com/problems/xuan-zhuan-shu-zu-de-zui-xiao-shu-zi-lcof/solution/xuan-zhuan-shu-zu-de-zui-xiao-shu-zi-by-leetcode-s/

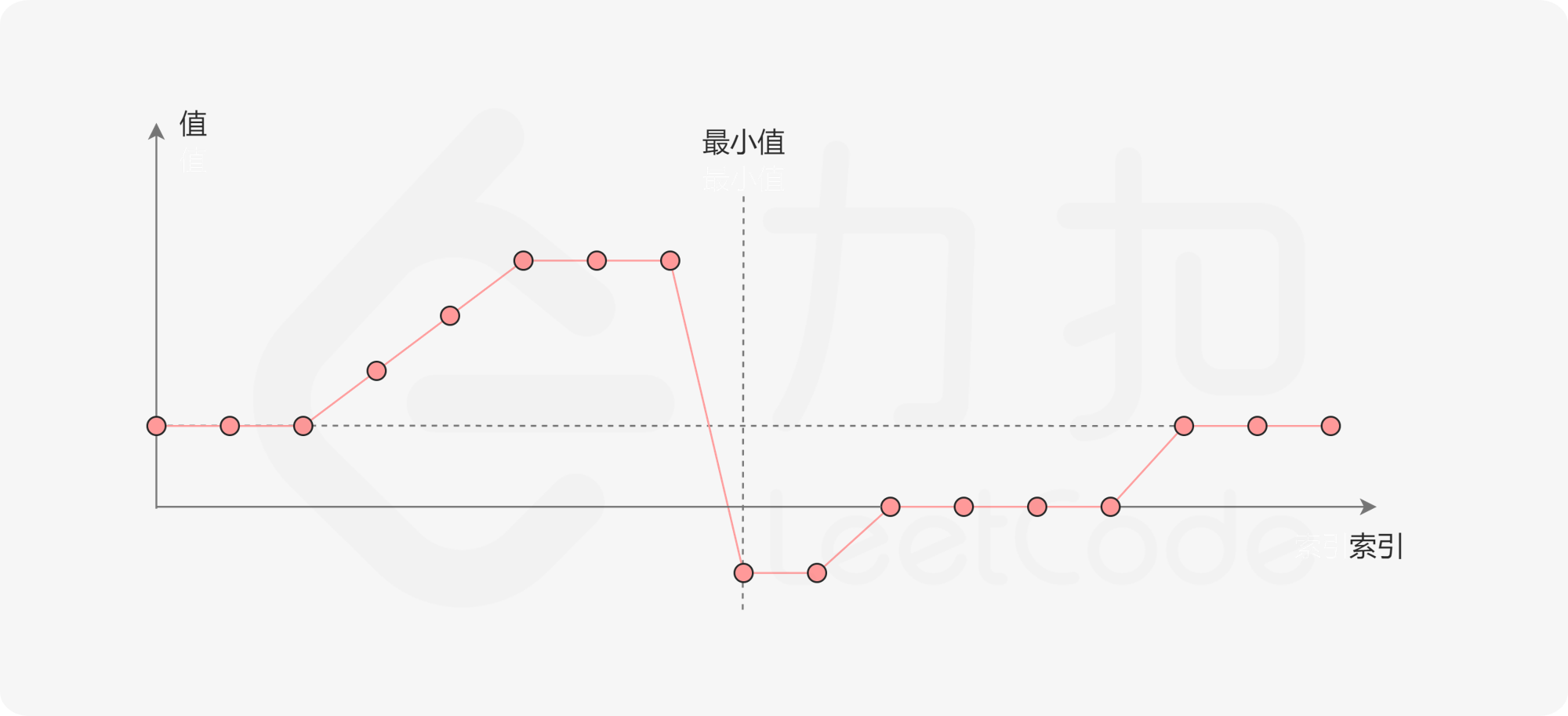
把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转，该数组的最小值为1。

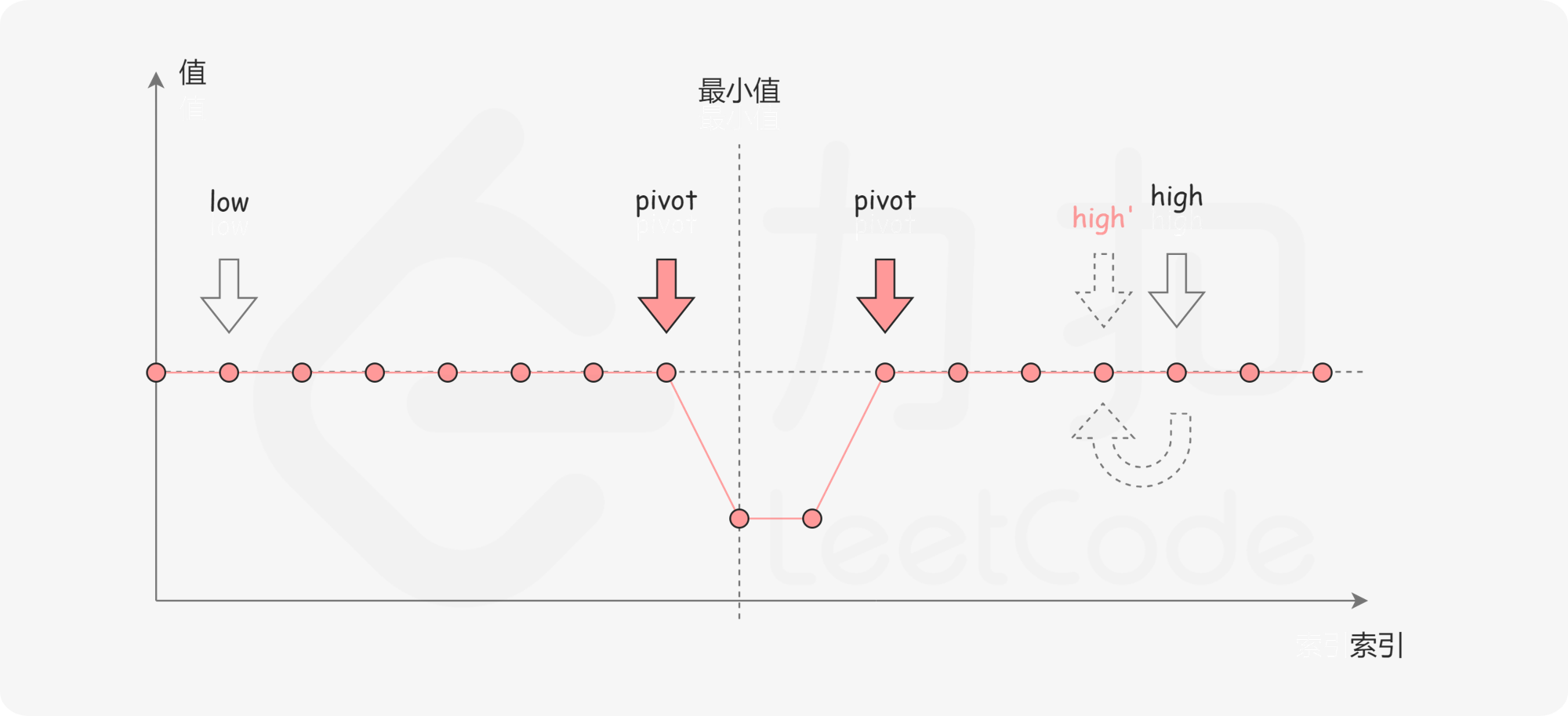
该问题的思路与上一题相似，都是先判断单调性，然后再进行二分，区别在于，这里是判断与 right 值的关系从而确定单调性。上一题是一直判断与 0 位置的关系从而确定单调性。

上一题是找目标值位置，这一题是找最小值

img

img

详细分析见官方题解。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public int minArrayTwoSperate(int[] numbers) {
    int left = 0;
    int right = numbers.length - 1;

    // 一直二分到left == right，此时的left就是要找的最小值
    while (left < right) {
        int mid = left + ((right - left) >> 1);

        // 只判断mid和right的关系就够了，不需要再去判断left
        // 因为右边如果正常，左边肯定异常，因此不需要判断左边界值
        if (numbers[mid] > numbers[right]) {    
            // 如果mid值大于right，说明右边有问题，更新左边界
            left = mid + 1;
        } else if (numbers[mid] < numbers[right]) {
            // 如果mid值小于right，说明右边是正常的，左边有问题，更新右边界
            right = mid;
        } else {
            // 如果mid==right，则无法判断最小值是在mid左还是右
            // 因为有可能 [4,3, 4 ,4,4] 或者 [4,4, 4 ,3,4]
            // ps: [5,3, 4 ,4,4] 也有可能
            // 这两种情况都满足mid==right，但是最小值在左还是右边无法确定
            // 所以right--，再进入下一次循环，更新mid的位置，从而找到最小值
            right--;
        } 
    }

    // left此时等于right
    return numbers[left];
}

在排序数组中查找数字

剑指 Offer 53 - I. 在排序数组中查找数字 I：统计一个数字在排序数组中出现的次数。

版本1：两次二分 + 单独变量保存左右边界：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
public int search(int[] nums, int target) {
    if (nums == null || nums.length == 0) {
        return 0;
    }

    if (nums[0] > target || nums[nums.length - 1] < target) {
        return 0;
    }

    int left = 0;
    int right = nums.length - 1;
    int mid = 0;
    // 记录左右边界
    int leftBound = -1;
    int rightBound = -1;

    while (left <= right) {
        mid = left + (right - left >> 1);
        if (nums[mid] == target) {
            leftBound = mid;
            right = mid - 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }

    if (left == -1) {
        return 0;
    }

    left = 0;
    right = nums.length - 1;
    mid = 0;
    while (left <= right) {
        mid = left + (right - left >> 1);
        if (nums[mid] == target) {
            rightBound = mid;
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }

    if (leftBound != -1 && rightBound != -1) {
        return rightBound - leftBound + 1;
    } else {
        return 0;
    }
}

版本2：合并等于与小于或大于：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
public int search(int[] nums, int target) {
    if (nums == null || nums.length == 0) {
        return 0;
    }

    if (nums[0] > target || nums[nums.length - 1] < target) {
        return 0;
    }

    int left = 0;
    int right = nums.length - 1;
    int mid = 0;
    // 记录左右边界
    int leftBound = -1;
    int rightBound = -1;

    while (left <= right) {
        mid = left + (right - left >> 1);
        if (nums[mid] >= target) {
            leftBound = mid;
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }

    if (left == -1) {
        return 0;
    }

    left = 0;
    right = nums.length - 1;
    mid = 0;
    while (left <= right) {
        mid = left + (right - left >> 1);
        if (nums[mid] <= target) {
            rightBound = mid;
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        }
    }

    if (leftBound != -1 && rightBound != -1) {
        return rightBound - leftBound + 1;
    } else {
        return 0;
    }
}

版本3：复用。可以参考 34. 在排序数组中查找元素的第一个和最后一个位置 与 剑指 Offer 53 - I. 在排序数组中查找数字 I 的题解

0～n-1中缺失的数字

剑指 Offer 53 - II. 0～n-1中缺失的数字：一个长度为n-1的递增排序数组中的所有数字都是唯一的，并且每个数字都在范围0～n-1之内。在范围0～n-1内的n个数字中有且只有一个数字不在该数组中，请找出这个数字。

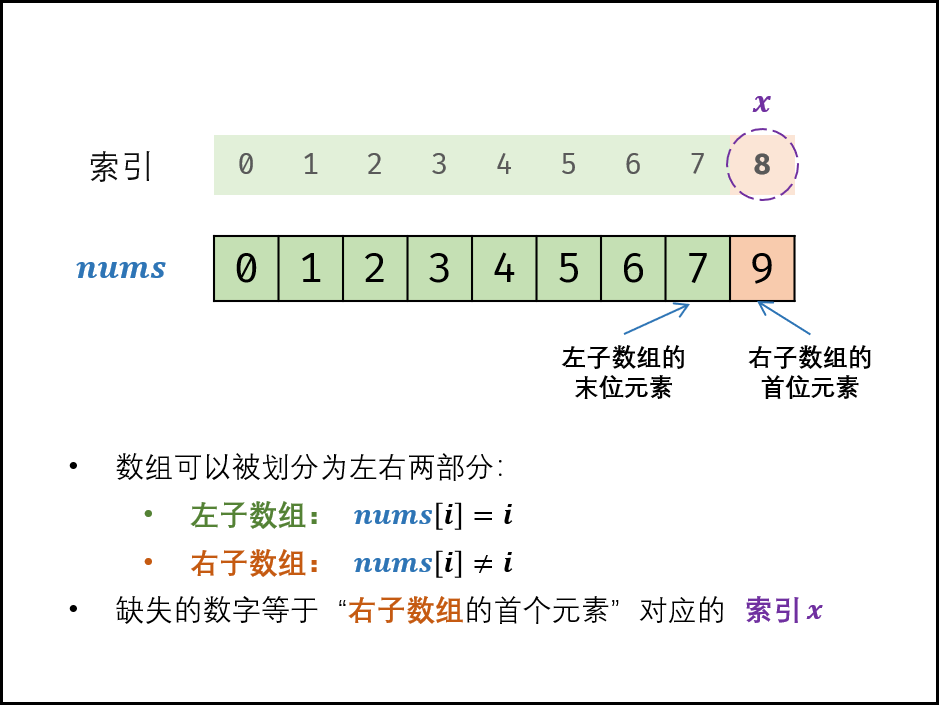
数组可以按照以下规则划分为两部分：

  • 左子数组：nums[i] = i
  • 右子数组：nums[i] ≠ i

缺失的数字等于 “右子数组的首位元素” 对应的索引；因此考虑使用二分法查找 “右子数组的首位元素” 。

Picture1.png

在二分循环时：

  • 若 nums[m] = m ，则 “右子数组的首位元素” 一定在闭区间 [m + 1, right] 中，因此执行 left = m + 1
  • 若 nums[m] ≠ m，则 “左子数组的末位元素” 一定在闭区间 [left, m - 1] 中，因此执行 right = m - 1

跳出循环时，变量 left 和 right 分别指向 “右子数组的首位元素” 和 “左子数组的末位元素”，并且 left= right + 1 。因此返回 left 即可。

这种思想非常好，适用于许多类型的二分问题。将整个数组分为两个区域：左子数组和右子数组，最后退出循环时

  • left 指向右子数组的首位元素，更新时 left = mid + 1
  • right 指向左子数组的末位元素，更新时 right = mid - 1

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public int missingNumber(int[] nums) {
    if (nums == null || nums.length == 0) {
        return 0;
    }
    int left = 0;
    int right = nums.length - 1;
    int mid = 0;
    while (left <= right) {
        mid = left + (right - left >> 1);
        if (nums[mid] == mid) {
            // 右子数组的首位元素（答案）肯定在 [mid + 1, right] 区间内
            left = mid + 1;
        } else {
            // 左子数组的末位元素肯定在 [left, mid - 1] 区间内
            right = mid - 1;
        }
    }
    // 退出时，left 指向右子数组的首位元素，也就是答案
    return left;
}

寻找峰值

162. 寻找峰值：峰值元素是指其值严格大于左右相邻值的元素。

给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。你可以假设 nums[-1] = nums[n] = -∞ 。

思路：当 nums[mid] 比左右都大，就说明他是峰值，直接返回，否则向更大的那一侧二分。注意，此时的二分范围是 [1, n-1]，要把两侧的给排除掉。注意：退出循环时需要额外判断一下 left 和 right 谁更大

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public int findPeakElement(int[] nums) {
    if (nums == null || nums.length == 0) {
        return -1;
    }
    // 当 nums[mid] 比左右都大，就说明他是峰值，直接返回
    // 否则向更大的那一侧二分。
    // 注意，此时的二分范围是 [1, n-1]，要把两侧的给排除
    
    // 先处理边界情况
    if (nums.length == 1) {
        return 0;
    } else if (nums.length == 2) {
        return nums[0] > nums[1] ? 0 : 1;
    }

    int left = 1;
    int right = nums.length - 2;
    int mid = 1;
    while (left <= right) {
        mid = left + (right - left >> 1);
        // 找到答案直接返回
        if (nums[mid] > nums[mid - 1] && nums[mid] > nums[mid + 1]) {
            return mid;
        } else if (nums[mid] < nums[mid - 1]) {
            // 如果左侧更大，则向左侧二分
            right = mid - 1;
        } else {
            // 如果右侧更大，向右侧二分
            left = mid + 1;
        }
    }
    // 退出循环时需要额外判断一下 left 和 right 谁更大
    return nums[left] > nums[right] ? left : right;
}

题解思路：使用模板二的思路，并不在找到时立即返回，而是最后再返回。该思路将判断左右改为只判断 nums[mid] 和 nums[mid + 1]，不需要判断左侧元素。代码更加简洁。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public int findPeakElement(int[] nums) {
    int left = 0;
    int right = nums.length - 1;
    int mid;
    // 这样能避免 mid + 1 越界
    // 退出时left==right，因此mid的上限也不会超过最大的right，也就等于 nums.length-1，所以肯定不会越界
    while (left < right) {
        mid = left + (right - left >> 1);
        // 此时已经保证了 mid+1 不会越界，但是不能保证 mid-1 不会越界
        // 因此我们只判断 mid 和 mid+1 的关系
        // 因为四种情况都可以总结为判断 mid 和 mid+1 的关系
        //  mid-1 < mid > mid+1  ---> 找到答案
        //  mid-1 < mid < mid+1  ---> 坡顶肯定在右侧，left = mid + 1
        //  mid-1 > mid < mid+1  ---> 坡顶可能在左也可能在右，随便走一个方向，比如右边，left = mid + 1
        //  mid-1 > mid > mid+1  ---> 坡顶肯定在左侧，right = mid。之所以不减一是因为要考虑上面第一种情况 mid-1 < mid > mid+1，这时的mid可能就是答案，不能跳过，除非不用模板二，而是在找到时直接返回，就不用再这样了

        // 综上，不需要考虑mid-1的大小（因为mid-1可能等于-1，越界），上述四种情况可以总结为和 mid+1 的关系的比较
        // mid > mid+1，就往左二分，mid < mid+1，就往右二分
        if (nums[mid] < nums[mid+1]) {
            // 坡顶在右侧，往右侧二分
            left = mid + 1;
        } else {
            // 坡顶在左侧（或者mid就是坡顶）
            right = mid; // 不减一是因为可能mid就是坡顶，不能忽略掉（即符合情况1）
        }
    }
    // 额外考虑 left == right 时的情况
    return left;
}

step sum

step sum 的定义：比如 680，680 + 68 + 6 = 754，则 680 的 step sum 为 754

给定一个正整数 target，判断他是否是某个数的 step sum，若是返回 true，若不是返回 false。

思路：某个数 x 的 stepSum(x) 肯定满足 x <= stepSum(x)，满足单调性。因此可以使用二分法，从区间 [0, target]，在其内不断二分，判断中点 mid 的 stepSum(mid) 与 target 的关系。

  • 若stepSum(mid) < target，则结果值 x 肯定在 mid 的右边
  • 若stepSum(mid) > target，则结果值 x 肯定在 mid 的左边
  • 若stepSum(mid) == target，则找到了结果值 x == mid
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 二分查找 [0, target] 范围内，某个数 x 的 stepSum(x) == target
// x <= stepSum(x)，满足单调性，可以使用二分
public boolean isStepSum(int target) {
   int left = 0;
   int right = target;
   int mid;

   while (left <= right) {
      mid = left + (right - left >> 1);
      if (stepSum(mid) < target) {
         // 如果小于，则要求的值一定在 mid 右边
         left = mid + 1;
      } else if (stepSum(mid) > target) {
         // 如果大于，则要求的值一定在 mid 左边
         right = mid - 1;
      } else {
         return true;
      }
   }
   return false;
}

// 计算 x 的 stepSum
public int stepSum(int x) {
   int sum = 0;
   while (x != 0) {
      sum += x;
      x /= 10;
   }
   return sum;
}

画家问题

题目：给定一个整型数组 nums，数组中的每个值都是正数，表示完成一幅画作需要的时间，在给定一个整数 num 表示画匠的数量，每个画匠只能画连在一起的画作。所有的画家并行工作，返回完成所有的画作需要的最少时间。

类似题目：410. 分割数组的最大值

注意：题目给的画家数 m 其实并不一定是最优分配情况下的画家数，而可能比最优数要大。例如在 m = 4 时的整体最小作画耗时和 m = 3 时的整体最小作画耗时可能是相等的，这一点体现在代码中的 need(nums, mid) <= m 里，很可能存在比当前最小作画耗时更短的情况下，需要的画家数量还更少，这种情况当然是满足题意的。

题目中的两个隐形要求：

  • 需要的画家数不能超过题目给定的画家数 m
  • 整体的最小作画耗时 h 要尽可能小

整体最小作画耗时 h 的分布区间：

  • 区间越往左侧，h 越小，需要的画家数量也越多，但可能不满足要求1（最小的 h 等于1）
  • 区间越往右侧，h 越大，需要的画家数量也越少，画家数量是可以满足题目要求，但是需要的耗时太大，可能不满足要求2（最大的 h 等于整个数组的累计和，代表一个画家画完所有画，是最费时的一种情况）

题目的目标就是在这个区间中尽可能左侧的位置（代表 h 尽可能小），找到一个满足要求1：画家数量不超过 m 的作画耗时值。

可以从上述规律中找出单调性：需要的画家越多，最大耗时越小。因此可以用二分法解决该问题。将求解最短作画耗时的问题转化为二分地判断当前最大作画耗时的情况下，需要几个画家：

  • 如果需要的画家多于题目给定的 m（不满足要求1），则说明当前要求的最大作画耗时太小了（太靠近区间左侧了），那么就二分增加该时间限制（向区间右侧二分）；
  • 如果需要的画家小于等于题目给定的 m（满足要求1），则当前的最大作画耗时是满足要求1的（更靠近区间右侧），但可能还不是最优的，还可能在区间左侧有一个更小的时间也是满足该时间对应的画家数量也是小于 m 的（要求1）。因此先记录下来当前时间值 ans，然后继续向左侧二分；
  • 直到不满足 left <= right，二分结束，返回此时记录的时间值 ans，就是既满足要求1，又满足要求2的答案值

这是一种逆向思维，将求时间限制的问题转换为：求哪种时间限制的情况下，需要的画家满足题目给定的条件。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
public int splitArray(int[] nums, int m) {
    // 画家问题
    // nums：需要完成的画
    // m：画家的个数
    
    // 先计算出一个画家画完所有画需要的时间 
    int sum = 0;
    for (int i = 0; i < nums.length; i++) {
        sum += nums[i];
    }

    // left 和 right 均代表时间限制，也就是要二分查找的结果
    int left = 1;
    int right = sum;
    int mid;
    int ans = 0;
    // 无限多的画家（对应二分区间里的最小值（耗时））肯定能得到最小的总耗时，但是题目不可能给这么多画家，所以必须 left 右移，
    // 只要一个画家（对应二分区间里的最大值（耗时））肯定需要耗费很多的时间，所以必须 right 左移

    while (left <= right) {
        // mid 代表的是最大耗时
        mid = left + (right - left >> 1);
        // 如果当前最大耗时所需要的画家数量比题目给定的还少
        // 说明可以继续增加画家数量，使得最大耗时进一步减少，因此向左二分
        // 注意要包含等于的情况
        if (need(nums, mid) <= m) {
            ans = mid;
            right = mid - 1;
        } else {
            // 如果当前最大耗时所需要的画家数量比题目给定的多
            // 说明需要减少画家数量，使得最大耗时增大，因此向右二分
            left = mid + 1;
        }
    }
    return ans;
}

// 根据最大作画时间 h 计算最少的画家个数 n
// 每一幅画需要的时间都在 nums 里，如果一定要求整体不超过 h 小时
// 那么返回需要的最少画家数量
public int need(int[] nums, int h) {
    for (int i = 0; i < nums.length; i++) {
        if (nums[i] > h) {
            // 如果某个时间大于了限制的最大作画时间
            // 则说明多少个画家都不可能完成
            // 返回系统最大值，代表无解
            return Integer.MAX_VALUE;
        }
    }

    // 需要的最少画家个数 parts
    int parts = 1;

    // 当前画家已经作画的时间
    // 注意，该时间需要先赋值为第一幅画的耗时
    // 从第二幅画开始遍历
    int currTime = nums[0];

    // 从第二幅画开始遍历
    for (int i = 1; i < nums.length; i++) {
        // 如果当前画家已经画的时间 currTime 加上当前画需要耗时后大于最大限制 h
        // 则代表需要一个新的画家画这幅画，当前画家的任务结束了，该另其一个新画家了
        if (currTime + nums[i] > h) {
            // 另起一个新的画家
            parts++;
            // 新画家的耗时设置为当前画的耗时
            currTime = nums[i];
        } else {
            // 如果不超出，则更新当前画家的作画总耗时
            currTime += nums[i];
        }
    }
    return parts;
}

峰值元素

https://leetcode-cn.com/problems/find-peak-element/solution/xun-zhao-feng-zhi-by-leetcode-solution-96sj/

该方法适用于模板二。

峰值元素是指其值严格大于左右相邻值的元素。

给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    public int findPeakElement(int[] nums) {
        int left = 0;
        int right = nums.length - 1;
        int mid;

        // 退出时left==right，因此mid的上限也不会超过最大的right，也就等于 nums.length-1，所以肯定不会越界
        // 这样能避免 mid + 1 越界
        while (left < right) {
            mid = left + (right - left >> 1);
            // 此时已经保证了 mid+1 不会越界，但是不能保证 mid-1 不会越界
            // 因此我们只判断 mid 和 mid+1 的关系
            // 因为四种情况都可以总结为判断 mid 和 mid+1 的关系
            //  mid-1 < mid > mid+1  ---> 找到答案
            //  mid-1 < mid < mid+1  ---> 坡顶肯定在右侧，left = mid + 1
            //  mid-1 > mid < mid+1  ---> 坡顶可能在左也可能在右，随便走一个方向，比如右边，left = mid + 1
            //  mid-1 > mid > mid+1  ---> 坡顶肯定在左侧，right = mid。之所以不减一是因为要考虑上面第一种情况 mid-1 < mid > mid+1，这时的mid可能就是答案，不能跳过，除非不用模板二，而是在找到时直接返回，就不用再这样了

            // 综上，不需要考虑mid-1的大小（因为mid-1可能等于-1，越界），上述四种情况可以总结为和 mid+1 的关系的比较
            // mid > mid+1，就往左二分，mid < mid+1，就往右二分
            if (nums[mid] < nums[mid+1]) {
                // 坡顶在右侧，往右侧二分
                left = mid + 1;
            } else {
                // 坡顶在左侧（或者mid就是坡顶）
                right = mid; // 不减一是因为可能mid就是坡顶，不能忽略掉
            }
        }

        // 额外考虑 left == right 时的情况
        return left;
    }
}

找到 K 个最接近的元素

658. 找到 K 个最接近的元素：给定一个排序好的数组 arr ，两个整数 k 和 x ，从数组中找到最靠近 x（两数之差最小）的 k 个数。返回的结果必须要是按升序排好的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
class Solution {
    public List<Integer> findClosestElements(int[] arr, int k, int x) {
        if (arr == null && arr.length < k) {
            return null;
        }
        int[] nums = arr;
        // 查找出来的结果放优先级队列里
        // 先二分查找到距离x最近的位置（左，右）
        // 对比左右边界哪个距离x更近，
        // 然后将最近的（左或右）放到优先级队列里（前提是count小于k），
        // 最后将队列里的数字取出来就是排好序的
        int left = 0;
        int right = arr.length - 1;
        int mid = 0;

        // 如果找到等于的，直接break，在此基础上进行寻找k个最小的数
        // 如果找不到等于的，则跳出循环时，mid肯定最接近x，但是可能在x左边，也可能在x右边
        while (left <= right) {
            mid = left + (right - left >> 1);
            if (nums[mid] == x) {
                // 只要数组中有和x相等的，在这一步肯定能找到
                break;
            } else if (nums[mid] < x) {
                left = mid + 1; // mid 小于 x，开始向右查找
            } else if (nums[mid] > x) {
                right = mid - 1;
            }
        } 

        // 出循环后，要么mid的位置等于x，要么mid在x的左，或者右（最接近x）
        // 通过mid值和x的大小找出mid是在x的左侧还是右侧
        // 找出来之后就可以确定第二个指针的位置了
        // 通过mid值和x大小的关系确定出三种情况下的双指针策略
        int l = 0;
        int r = 0;
        // 其实不需要heap，只需要最后得到l和r就可以得到list了
        Queue<Integer> heap = new PriorityQueue<>();
        if (nums[mid] == x) {
            // 如果相等，则先将mid位置进优先队列，然后设置左右指针
            heap.add(nums[mid]);
            k--;
            l = mid - 1;
            r = mid + 1;
        } else if (nums[mid] < x) {
            // 如果mid小于x，则mid是左指针，mid+1是右指针
            l = mid;
            r = mid + 1;
        } else if (nums[mid] > x) {
            l = mid - 1;
            r = mid;
        }

        // 双指针 l 和 r 移动时先判断谁更小，更小的进队列
        // 注意边界条件
        while (k-- > 0) {
            // 循环k次，将k个数入堆
            // 故意设置左指针减去x的值为正数，代表左指针越界
            // 故意设置右指针减去x的值为负数，代表右指针越界
            int lDiff = 1;
            int rDiff = -1;
            if (l >= 0) {
                lDiff = nums[l] - x;
            }
            if (r < nums.length) {
                rDiff = nums[r] - x;
            }

            // 说明都正常
            if (lDiff <= 0 && rDiff >= 0) {
                if (Math.abs(lDiff) <= Math.abs(rDiff)) {
                    // 当前更小值入堆
                    heap.add(nums[l]);
                    l--;
                } else {
                    heap.add(nums[r]);
                    r++;
                }
            } else if (lDiff == 1 && rDiff != -1) {
                // 说明左侧越界，右侧没越界
                heap.add(nums[r]);
                r++;
            } else if (rDiff == -1 && lDiff != 1) {
                heap.add(nums[l]);
                l--;
            }
        }

        List<Integer> list = new ArrayList<>();
        // 最后将heap变成数组
        while (!heap.isEmpty()) {
            list.add(heap.poll());
        }
        return list;

        // 题解里的思路：先用模板二right=mid找出最接近x的右侧的与元素
        // 然后比较该元素和其左边元素谁更接近目标值，从而确定index
        // 确定之后，使得l和r在index两侧不断向两侧展开
        // 知道r和l组成的开区间(l,r)内的元素个数等于k，跳出循环
        // 说明找到了(l,r)内的k个元素，就是答案，注意，l和r组成的是开区间，不要把二者包含进去

        int leftindex = index-1;
        int rightindex = index+1;
        while(rightindex-leftindex-1<k){
            if(leftindex<0){
                rightindex++;
                continue;
            } 
            if(rightindex>=len){
                leftindex--;
                continue;
            } 
            if(x-arr[leftindex]<=arr[rightindex]-x) leftindex--;
            else rightindex++;
        }
    }
}