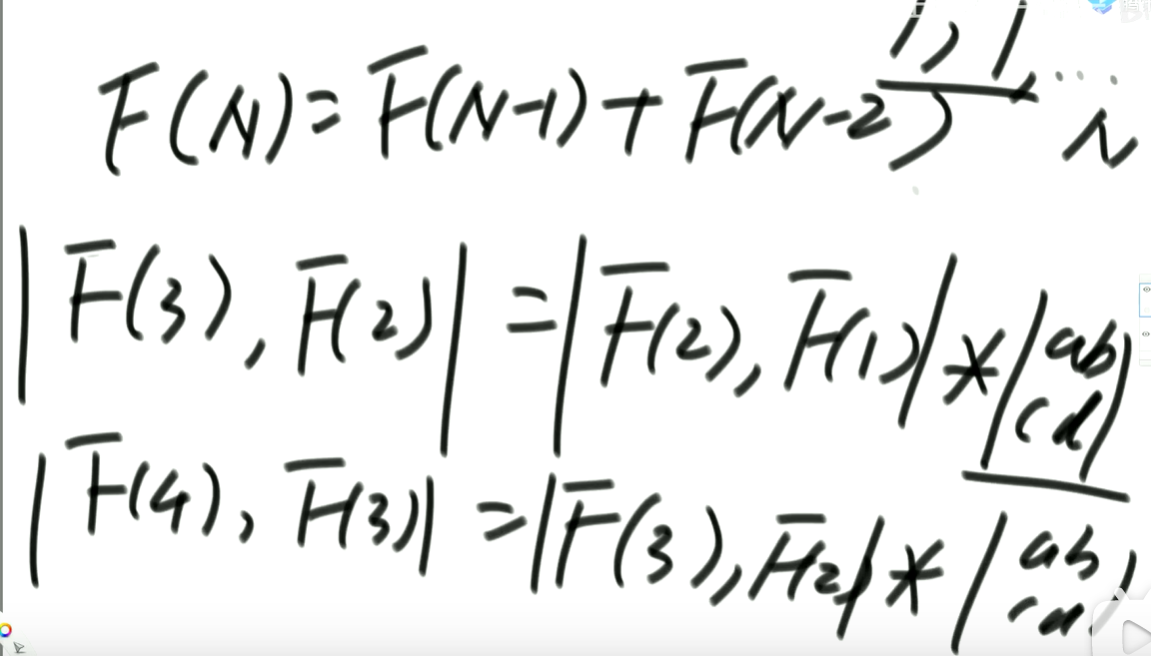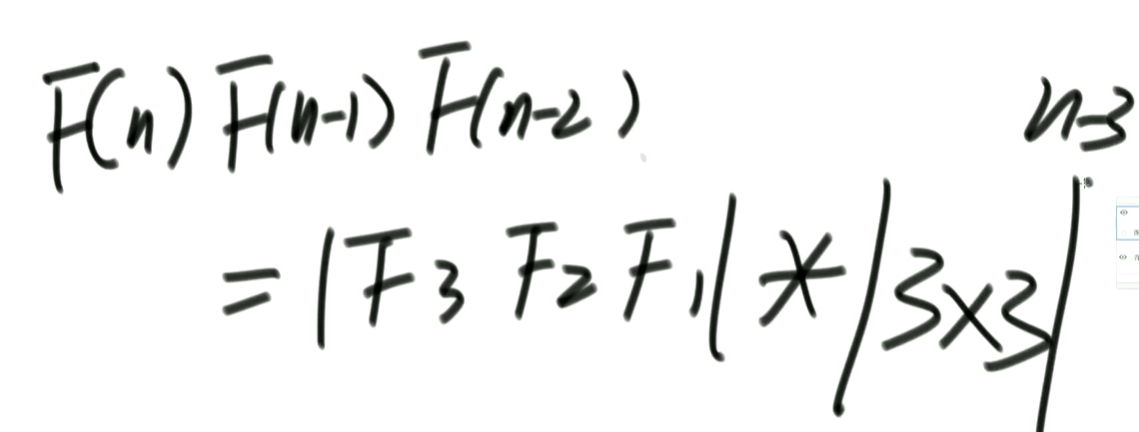【算法】动态规划

发表于2021-11-28更新于2022-03-04字数统计15.1k阅读时长108分阅读次数

动态规划的思想

首先进行暴力尝试，然后建立记忆搜索表进行缓存，最后建立严格表结构。

直接使用暴力递归，会将所有情况都进行尝试，这样时间复杂度较高，有很多之前尝试过的答案会在其他分支仍然进行尝试。因此可以在暴力递归的基础上建立记忆搜索表（缓存表），将已经尝试过的答案缓存到表中，这样在其他分支就不需要再次尝试了，可以直接从基友搜索表里获取结果，从而节省了大量的时间，该方法又被称为记忆化递归法。最后可以根据暴力尝试的推导公式建立严格表结构，从而省去递归操作，在严格表中通过递推快速得到结果。

暴力递归就是尝试：

  • 把问题转化为规模缩小了的同类问题的子问题
  • 有明确的不需要继续进行递归的条件（base case）
  • 有当得到了子问题的结果之后的决策过程
  • 不记录每一个子问题的解

暴力递归的常用技巧：

  • 在递归过程中不保存结果，而是在调用到 base case（栈底）时才执行保存，因为到 base case 时说明当前这条路是走得通的，那么走到底时就可以保存结果了，如果某条路走不通（例如八皇后问题中可能某些路就走不通）则不会到 base case，从而不会保存。
  • 在递归过程中通过修改 char[] 或 int[] 里的值来节省空间，在调用子问题前先修改原数组（要注意暂存起来修改前的值），并在子问题执行完毕后将其原始值保存回去，从而做到保持原数组的正确性，不影响其他的递归栈

上述技巧使用举例：例如要保存一个字符串的所有子序列：

  • 递归过程中在修改 char[] 数组当前位置的值为空 ''，代表不考虑当前字符的情况，修改后进入子问题，得到不考虑当前位置字符时的结果；然后该子问题的方法栈调用完毕后，再将原始值赋值回去，再调用一次子问题，代表考虑当前字符的情况，又可以得到一种结果
  • 递归到底时，再保存当前 char[] 中的内容到结果列表里。

动态规划常见题目

背包问题

给定两个长度都为N的数组weights和values，weights[i]和values[i]分别代表i号物品的重量和价值。给定一个正数bag，表示一个载重bag的袋子，你装的物品不能超过这个重量。返回你能装下最多的价值是多少？

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
package com.zhao;

public class Knapsack {
    public static int maxValue(int[] weights, int[] values, int bag) {
        return process(0, weights, values, 0, 0, bag);
    }

    public static int process(int i, int[] weights, int[] values, int alreadyWeight, int alreadyValue, int bag) {
        // 如果当前重量已经超了，则不需要再继续递归了，下面肯定不满足了
        if (alreadyWeight > bag) {
            // 如果发现当前的重量超了，说明上一层调用时，前一个袋子里的重量加上去就超了，
            // 所以当前层以后的都不用考虑了，因为肯定会超出限制，直接返回，并且返回的总价值要减去上层的价值，
            // 代表上层不能将其重量算进去，否则就超了。也就是说上一层的分支止步于此了，
            // 这条分支选择拿了上一层的values[i-1]物品，发现超了，也就是说不能拿这个物品，
            // 所以该分支止步于此了，其最大值就是 alreadyValue - values[i-1]（因为alreadValue里多算了values[i-1]，这个是不能算进去的，因为会导致超出重量限制
            return alreadyValue - values[i - 1];
            // 也可以 return 0
        }

        if (i == weights.length) {
            // base case
            return alreadyValue;
        }

        // 1. 加上当前重量
        // 2. 不加上当前重量
        // 返回两种情况的最大值
        // 注意：在这里并没有考虑加上当前层后是否会超出重量限制，所以需要在下一层先判断alreadyWeight是否大于bag，
        // 如果大于，这条添加当前物品的分支就止步于此了，返回的价值要减去当前加上的values[i]，体现在代码第一行的判断
        return Math.max(
            process(i + 1, weights, values, alreadyWeight + weights[i], alreadyValue + values[i], bag),
            process(i + 1, weights, values, alreadyWeight, alreadyValue, bag)
        );
        
        // 可以改为记忆化搜索版本，借助record[]记录当前i位置的最大value值
    }

    // 动态规划版
    public static int maxValue2(int[] weights, int[] values, int bag) {
        int[][] dp = new int[weights.length + 1][bag + 1];
        for (int i = weights.length - 1; i >= 0; i--) {
            for (int j = bag; j >= 0; j--) {
                dp[i][j] = dp[i + 1][j];
                if (j + weights[i] <= bag) {
                    dp[i][j] = Math.max(dp[i][j], values[i] + dp[i + 1][j + weights[i]]);
                }
            }
        }
        return dp[0][0];
    }

    public static void main(String[] args) {
        int[] weights = { 4, 7, 6, 8 };
        int[] values = { 5, 6, 3, 19 };
        int bag = 11;
        System.out.println(maxValue(weights, values, bag));
        System.out.println(maxValue2(weights, values, bag));
    }
}

背包问题 II

牛牛准备参加学校组织的春游，出发前牛牛准备往背包里装入一些零食，牛牛的背包容量为w。

牛牛家里一共有n袋零食，第i袋零食体积为v[i]。牛牛想知道在总体积不超过背包容量的情况下，他一共有多少种零食放法（总体积为0也算一种放法）。

纸牌游戏

给定一个整型数组arr，代表数值不同的纸牌排成一条线。玩家A和玩家B依次拿走每张纸牌，规定玩家A先拿，玩家B后拿，但是每个玩家每次只能拿走最左或最右的纸牌，玩家A和玩家B都绝顶聪明。请返回最后获胜者的分数。

image-20211129181112430

思路：将整个抽牌过程拆成先手和后手两种策略。

  • 己方先作为先手抽牌，有两种情况，取这两种情况的最大点数情况
    • 抽最左侧的牌，然后己方作为后手等待对方抽一张
    • 抽最右侧的牌，然后己方作为后手等待对方抽一张
  • 己方作为后手时是不能抽牌的，要等对方抽完一张后己方再作为先手抽牌，此时流程又回到了己方作为先手抽牌的情况。对方有两种抽法，己方要取两种先手情况的最小值。因为对方肯定会抽掉某张牌，使得己方再作为先手抽剩下的牌时得分最少，所以是取最小值

代码中将不断递归地在先手方法里调用后手方法，在后手方法里递归地调用先手方法，直到就剩一张牌，此时：

  • 己方若为先手，则抽到这张牌，返回该值，递归栈开始返回
  • 己方若为后手，则不能抽到这张牌，返回0，递归栈开始返回

需要注意的是，己方作为后手时是不能抽牌的，要直接返回去掉两侧牌后的两种先手情况的最小值。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
public class CardsInLine {
    public static int maxScore01(int[] nums) {
        if (nums == null || nums.length == 0) {
            return 0;
        }
        // 我们不知道最大得分是先手赢还是后手赢，所以都要尝试，取最大值
        return Math.max(first(nums, 0, nums.length - 1), second(nums, 0, nums.length - 1));
    }

    // 先手方法：己方先抽时能抽到的点数，肯定是任自己选择的
    // 要么抽取第i张牌（最左侧），要么抽取第j张牌（最右侧），那么策略就是取这两种方式里总点数最大的
    // 当前剩余牌的区间 [i, j]
    public static int first(int[] nums, int i, int j) {
        if (i == j) {
            // 只剩一张牌了，先手只能抽这张牌
            return nums[i];
        }

        // 1. 抽取第i张牌（最左侧）：nums[i] + second(nums, i + 1, j)
        // 2. 要么抽取第j张牌（最右侧）：nums[j] + second(nums, i, j - 1)
        // 因为是己方先手，所以肯定抽到两个策略里的最大值
        return Math.max(nums[i] + second(nums, i + 1, j), nums[j] + second(nums, i, j - 1));
    }

    // 后手方法：己方在对方抽取一张牌后再抽时能得到的点数，自己是不能选择的
    // 因为后手的优先权是在对方手里的，对方肯定会抽令自己优势最大的，因此己方的后手方法返回的是两种策略里的最小值
    public static int second(int[] nums, int i, int j) {
        // 己方后手时如果发现牌就剩一张了，那肯定被对方抽走了，自己后手留下的点数就是0
        if (i == j) {
            return 0;
        }

        // 1. 抽取第i张牌（最左侧）：nums[i] + second(nums, i + 1, j)
        // 2. 要么抽取第j张牌（最右侧）：nums[j] + second(nums, i, j - 1)
        // 之所以是min的原因是，最大的总点数的情况是被对方抽走的，自己只能剩下两种策略里的最小值
        // 因为是己方后手，所以肯定抽到两个策略里的最小值
        // 注意！！！这里不能加nums[i]，因为自己后手是不能抽牌的，是对方抽一张，然后自己作为先手再抽（即执行first()）
        return Math.min(first(nums, i + 1, j), first(nums, i, j - 1));
    }

    public static int win2(int[] arr) {
        if (arr == null || arr.length == 0) {
            return 0;
        }
        int[][] f = new int[arr.length][arr.length];
        int[][] s = new int[arr.length][arr.length];
        for (int j = 0; j < arr.length; j++) {
            f[j][j] = arr[j];
            for (int i = j - 1; i >= 0; i--) {
                f[i][j] = Math.max(arr[i] + s[i + 1][j], arr[j] + s[i][j - 1]);
                s[i][j] = Math.min(f[i + 1][j], f[i][j - 1]);
            }
        }
        return Math.max(f[0][arr.length - 1], s[0][arr.length - 1]);
    }

    public static void main(String[] args) {
        int[] arr = { 1, 9, 1 };
        System.out.println(maxScore01(arr));
        System.out.println(win2(arr));
    }
}

青草游戏

牛牛和羊羊都很喜欢青草，今天他们决定玩青草游戏。最初有一个装有n份青草的箱子，牛牛和羊羊依次进行，牛牛先开始。在每个回合中，每个玩家必须吃一些箱子中的青草，所吃的青草份数必须是4的x次幂，比如1，4，16，64等等。不能在箱子中吃到有效份数青草的玩家落败。假定牛牛和羊羊都是按照最佳方法进行游戏，请输出胜利者的名字。

思路：

  • 先枚举 n <= 4 时的胜负情况。
  • 然后先手第一次选择吃 1 份，判断此时剩余的草让对方成为先手开始吃胜负属于谁；
  • 如果自己胜利则直接返回，否则先手第一次选择吃 4 份，继续判断此时剩余的草让对方成为先手开始吃胜负属于谁；
  • 如果仍然是对方胜利，则先手第一次选择吃 16 份，继续判断此时剩余的草让对方成为先手开始吃胜负属于谁；
  • 重复以上过程，如果先手第一次无论吃多少份，赢得都是后手，代表先手不可能获胜，答案就是后手。如果中途有一次能让先手获胜，则答案就是先手。
  • 母过程的先手和子过程里的后手是同一个人，如果子过程的后手赢了，就代表母过程的先手赢了

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
public class EatGlass {

    public static String winner01(int n) {
        if (n >= 0 && n <= 4) {
            // 0  1  2  3  4
            // 后 先 后 先 先
            return (n == 0 || n == 2) ? "后手" : "先手";
        }

        /*
         * n >= 5 时, 先手决定吃的草的数量
         * 从 1 开始尝试, 先手吃 1 份草的情况下, 递归后续情况判断是谁赢
         * 如果先吃 1 份草先手无法赢, 则开始翻倍变为吃 4 份, 再递归后续情况判断是谁赢
         * 如果还不能赢, 则继续乘以 4. 重复该过程知道 base > n,
         * 如果这个过程中先手始终无法赢, 则答案就是后手赢
         */
        int base = 1;
        while (base <= n) {
            // 先手吃掉 base 份后, 还剩下 n - base 份, 此时递归判断在这种情况下是先手赢还是后手赢
            // 母过程的先手和子过程里的后手是同一个人, 如果子过程的后手赢了, 就代表母过程的先手赢了
            if ("后手".equals(winner01(n - base))) {
                return "先手";
            }
            // 防止 base * 4 后溢出整数范围, 从而造成死循环, 因此提前跳出
            if (base > n / 4) {
                break;
            }
            base *= 4;
        }
        return "后手";
    }

    // 打表:
    public static String winner02(int n) {
        if (n % 5 == 0 || n % 5 == 2) {
            return "先手";
        } else {
            return "后手";
        }
    }

    public static void main(String[] args) {
        // 遍历找规律
        for (int i = 0; i <= 50; i++) {
            System.out.println(i + " " + winner01(i));
        }
    }
}

机器人的运动范围

剑指 Offer 13. 机器人的运动范围：地上有一个m行n列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于k的格子。例如，当k为18时，机器人能够进入方格 [35, 37] ，因为3+5+3+7=18。但它不能进入方格 [35, 38]，因为3+5+3+8=19。请问该机器人能够到达多少个格子？

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public int movingCount(int m, int n, int k) {
    int[][] record = new int[m][n];
    movingCountHelper(0, 0, m, n, k, record);
    return count;
}
public int count = 0;

public void movingCountHelper(int i, int j, int m, int n, int k, int[][] record) {
    // 如果超出了边界，返回
    if (i < 0 || i >= m || j < 0 || j >= n) {
        return;
    }
    // 如果当前坐标和超过了k，也直接返回
    if (!isValid(i, j, k)) {
        return;
    }
    // 当前格子已经访问过，则不在继续访问
    if (record[i][j] == 1) {
        return;
    }

    // 设置当前为访问过
    record[i][j] = 1;
    count++;
    movingCountHelper(i - 1, j, m, n, k, record);
    movingCountHelper(i, j - 1, m, n, k, record);
    movingCountHelper(i + 1, j, m, n, k, record);
    movingCountHelper(i, j + 1, m, n, k, record);
}

// return true：符合条件
public boolean isValid(int i, int j, int k) {
    int sum = 0;
    // 计算i与j的位数和
    while (i != 0) {
        sum += i % 10;
        i /= 10;
    }
    while (j != 0) {
        sum += j % 10;
        j /= 10;
    }
    return sum <= k;
}

构建乘积数组

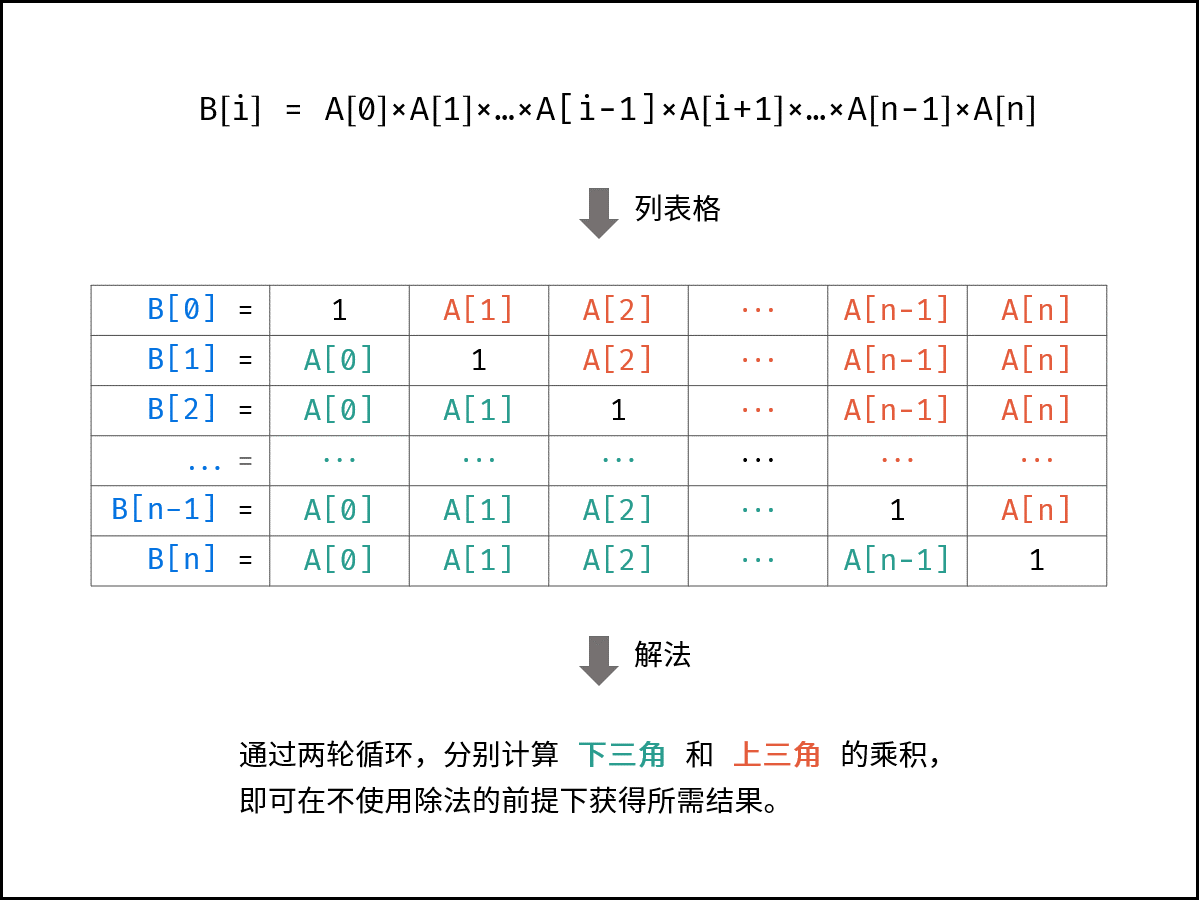
剑指 Offer 66. 构建乘积数组：给定一个数组 A[0,1,…,n-1]，请构建一个数组 B[0,1,…,n-1]，其中 B[i] 的值是数组 A 中除了下标 i 以外的元素的积, 即 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。

示例:

1
2
输入: [1,2,3,4,5]
输出: [120,60,40,30,24]

根据表格的主对角线（全为 11 ），可将表格分为 上三角 和 下三角 两部分。分别迭代计算下三角和上三角两部分的乘积，即可 不使用除法 就获得结果。

Picture1.png

算法流程：

  1. 初始化：数组 B，其中 B[0] = 1；辅助变量 tmp = 1；
  2. 计算 B[i] 的 下三角 各元素的乘积，直接乘入 B[i]；
  3. 计算 B[i] 的 上三角 各元素的乘积，记为 tmp，并乘入 B[i]；

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int[] constructArr(int[] a) {
        if (a == null || a.length == 0) {
            return new int[0];
        }
        // 1. 正向遍历数组，计算出b[]数组，b[i]代表当前位置i左侧的积（[0, i-1]相乘），
        // 2. 再反向遍历数组，当前位置左侧的积为b[i]，再乘以右侧的积（该值在反向遍历的过程中不断更新为[i+1, N]上的乘积） 
        int[] b = new int[a.length];
        // 最后一个元素的左侧积为1
        b[0] = 1;
        for (int i = 1; i < a.length; i++) {
            // a[i - 1]：当前位置左侧的值
            // b[i - 1]：当前位置左侧元素的左侧的积
            // 二者相乘即为当前位置左侧的积
            b[i] = b[i - 1] * a[i - 1];
        }

        int[] res = new int[a.length];
        // 最后一个元素的右侧积为1
        int tmp = 1;
        for (int i = a.length - 1; i >= 0; i--) {
            // 当前值 = 左侧的积 * 右侧的积
            res[i] = b[i] * tmp;
            // 更新右侧的积
            tmp = tmp * a[i];
        }
        return res;
    }
}

戳气球

312. 戳气球：有 n 个气球，编号为0 到 n - 1，每个气球上都标有一个数字，这些数字存在数组 nums 中。现在要求你戳破所有的气球。戳破第 i 个气球，你可以获得 nums[i - 1] * nums[i] * nums[i + 1] 枚硬币。这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号。如果 i - 1或 i + 1 超出了数组的边界，那么就当它是一个数字为 1 的气球。求所能获得硬币的最大数量。

示例 1：

1
2
3
4
5
输入：nums = [3,1,5,8]
输出：167
解释：
nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins =  3*1*5    +   3*5*8   +  1*3*8  + 1*8*1 = 167

思路：尝试的依据：当前位置必须是最后一个戳的情况下，整体获得的硬币数量。那么只需要先递归地计算左侧区域的硬币数（代表先戳破左边），再递归地计算右侧区域的硬币数（代表再戳破右边），最后只剩下当前一个气球，将其戳破，即可得到当前位置最后一个戳破整体可以得到的硬币数量。在戳左侧区域时，右边界就是当前位置；在戳右侧区域时，左边界就是当前位置。

其中，需要先构造辅助数组，在数组的左右边界额外补充两个1，这样在某个数组中的气球最后戳的时候也能顺利通过 L - 1 和 R + 1 得到当前戳得到的硬币：1 * nums[i] * 1，否则还得考虑边界条件，非常麻烦。

递归方法里需要将当前区间 [L, R] 内的位置一一尝试进行计算，会有大量重复计算，因此构建缓存表避免重复计算。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution {
    public int maxCoins(int[] nums) {
        // 先构造辅助数组，在数组的左右边界加上1，这样在某个数组中的气球最后戳的时候也能顺利通过L-1和R+1得到当前戳得到的硬币：1 * nums[i] * 1，否则还得考虑边界条件，非常麻烦
        int[] help = new int[nums.length + 2];
        help[0] = 1;
        help[nums.length + 1] = 1;
        for (int i = 0; i < nums.length; i++) {
            help[i + 1] = nums[i];
        }

        int[][] record = new int[help.length][help.length];
        // 原数组的值在[1, nums.length+1]范围内
        // 使用记忆化搜索算法：在该方法内遍历每一个位置，计算出当前位置最后戳的情况下得到的硬币数量，最后取最大值返回即可得到答案
        // 尝试的依据：当前位置必须是最后一个戳的情况下，整体获得的硬币数量
        return maxCoinsRecur(help, 1, nums.length, record);
    }

    // 计算当前区间 [L, R] 内，哪个位置的气球被最后戳爆可以得到的最大收益
    public int maxCoinsRecur(int[] nums, int L, int R, int[][] record) {
        // base case: 当只需要戳爆一个气球时，得到的硬币就等于该值乘以左侧和右侧的值
        if (L >= R) {
            return nums[L - 1] * nums[L] * nums[R + 1];
        }
        // 
        if (record[L][R] != 0) {
            return record[L][R];
        }
        int res = 0;
        int coins = 0;

        // 先计算两个边界情况：i == L 与 i == R
        // 这两个位置因为只有一侧需要计算，另一侧是不需要的，如果计算递归则会发生越界错误
        // 1. i == L，只需要计算右侧
        int coins1 = maxCoinsRecur(nums, L + 1, R, record) + nums[L - 1] * nums[L] * nums[R + 1];
        // 2. i == R，只需要计算左侧
        int coins2 = maxCoinsRecur(nums, L, R - 1, record) + nums[L - 1] * nums[R] * nums[R + 1];
        res = Math.max(coins1, coins2);

        for (int i = L + 1; i <= R - 1; i++) {
            coins = maxCoinsRecur(nums, L, i - 1, record) + maxCoinsRecur(nums, i + 1, R, record) + nums[L - 1] * nums[i] * nums[R + 1];
            res = Math.max(res, coins);
        }
        record[L][R] = res;
        return res;
    }
}

矩阵的最小路径之和

剑指 Offer II 099. 最小路径之和：给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。说明：一个机器人每次只能向下或者向右移动一步。

思路：本题是典型的动态规划问题，当前位置 [i][j] 的路径值 grid[i][j] ，要么选择加上左侧位置 [i][j - 1]，要么选择加上右侧位置 [i - 1][j]，因此最简单的想法就是从左到右，从上到下，遍历整个二维矩阵，不断更新当前位置的值：

1
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + m[i][j];

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public static int minPathSum1(int[][] m) {
    if (m == null || m.length == 0 || m[0] == null || m[0].length == 0) {
        return 0;
    }
    int row = m.length;
    int col = m[0].length;
    int[][] dp = new int[row][col];
    dp[0][0] = m[0][0];
    // 先初始化第一行
    for (int i = 1; i < row; i++) {
        dp[i][0] = dp[i - 1][0] + m[i][0];
    }
    // 再初始化第一列
    for (int j = 1; j < col; j++) {
        dp[0][j] = dp[0][j - 1] + m[0][j];
    }
    // 然后开始更新其他行和其他列，按照从左到右，从上到下的顺序遍历
    for (int i = 1; i < row; i++) {
        for (int j = 1; j < col; j++) {
            dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + m[i][j];
        }
    }
    // 返回右下角的值
    return dp[row - 1][col - 1];
}

但其实可以对该方法进行空间压缩优化：只使用一个一维数组，不断在该数组中更新路径和：从 arr[j - 1]（本行更新后的值） 和 arr[j]（上一行的旧值）中选出最小的更新到 arr[j] 里。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public int minPathSum(int[][] grid) {
    if (grid == null || grid.length < 1 || grid[0] == null || grid[0].length < 1) {
        return 0;
    }
    // 空间压缩技巧，只使用一个一维数组，例如长度等于 grid 的列数
    int[] arr = new int[grid[0].length];
    // 初始化该数组为 grid 的第一行元素，注意需要更新累加和
    arr[0] = grid[0][0];
    for (int j = 1; j < grid[0].length; j++) {
        arr[j] = grid[0][j] + arr[j - 1];
    }
    // 从第二行开始遍历，不断使用之前的 arr[i] 和 grid[i][j] 更新出新的 arr[i]
    for (int i = 1; i < grid.length; i++) {
        // 单独更新第一列，因为其左侧没有路可以选
        arr[0] = grid[i][0] + arr[0];
        // 然后逐个更新其他列，从 arr[j - 1]（本行更新后的值） 和 arr[j]（上一行的旧值）中选出最小的更新到 arr[j] 里
        for (int j = 1; j < grid[0].length; j++) {
            arr[j] = grid[i][j] + Math.min(arr[j], arr[j - 1]);
        }
    }
    return arr[grid[0].length - 1];
}

第

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


public static int minPathSum2(int[][] m) {
    if (m == null || m.length == 0 || m[0] == null || m[0].length == 0) {
        return 0;
    }
    int more = Math.max(m.length, m[0].length); // �����������ϴ���Ǹ�Ϊmore
    int less = Math.min(m.length, m[0].length); // ������������С���Ǹ�Ϊless
    boolean rowmore = more == m.length; // �����Dz��Ǵ��ڵ�������
    int[] arr = new int[less]; // ��������ij��Ƚ�Ϊ�����������е���Сֵ
    arr[0] = m[0][0];
    for (int i = 1; i < less; i++) {
        arr[i] = arr[i - 1] + (rowmore ? m[0][i] : m[i][0]);
    }
    for (int i = 1; i < more; i++) {
        arr[0] = arr[0] + (rowmore ? m[i][0] : m[0][i]);
        for (int j = 1; j < less; j++) {
            arr[j] = Math.min(arr[j - 1], arr[j])
                + (rowmore ? m[i][j] : m[j][i]);
        }
    }
    return arr[less - 1];
}

动态规划空间压缩技巧

如果某个动态规划问题的抽象网格模型中，当前位置 (i, j) 的更新只依赖于相邻的行和列的值，那么通常可以仅使用一个一维数组存储每一行或每一列更新的值。将更新二维表的过程修改为更新一维数组的过程，从而大大节省时间。

具体为存储行还是存储列取决于问题中的二维矩阵是行的尺寸比较大还是列的尺寸比较大。

  1. 当前位置依赖于左侧和上侧：

image-20220218210719946

  1. 当前位置取决于上侧、左上侧和左左上侧（此时需要从右往左遍历更新）：

image-20220218210937336

  1. 当前位置取决于左侧、上侧和左上侧（此时需要一个临时变量 t 先保存左上角的值，添加完再更新为当前位置的值）：

image-20220218210751063

空间压缩技巧例题：剑指 Offer 47. 礼物的最大价值

在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
// 未压缩
public static int minPathSum1(int[][] m) {
    if (m == null || m.length == 0 || m[0] == null || m[0].length == 0) {
        return 0;
    }
    int row = m.length;
    int col = m[0].length;
    int[][] dp = new int[row][col];
    dp[0][0] = m[0][0];
    for (int i = 1; i < row; i++) {
        dp[i][0] = dp[i - 1][0] + m[i][0];
    }
    for (int j = 1; j < col; j++) {
        dp[0][j] = dp[0][j - 1] + m[0][j];
    }
    for (int i = 1; i < row; i++) {
        for (int j = 1; j < col; j++) {
            dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + m[i][j];
        }
    }
    return dp[row - 1][col - 1];
}

// 压缩技巧
public static int minPathSum2(int[][] m) {
    if (m == null || m.length == 0 || m[0] == null || m[0].length == 0) {
        return 0;
    }
    int more = Math.max(m.length, m[0].length); 
    int less = Math.min(m.length, m[0].length); 
    boolean rowmore = more == m.length;
    int[] arr = new int[less];
    arr[0] = m[0][0];
    for (int i = 1; i < less; i++) {
        arr[i] = arr[i - 1] + (rowmore ? m[0][i] : m[i][0]);
    }
    for (int i = 1; i < more; i++) {
        arr[0] = arr[0] + (rowmore ? m[i][0] : m[0][i]);
        for (int j = 1; j < less; j++) {
            arr[j] = Math.min(arr[j - 1], arr[j])
                + (rowmore ? m[i][j] : m[j][i]);
        }
    }
    return arr[less - 1];
}

斐波那契系列问题

斐波那契数列

剑指 Offer 10- I. 斐波那契数列：写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下：

1
2
F(0) = 0,   F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.

斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

版本一：暴力递归

直接暴力递归时间复杂度过高，因为重复计算了大量的值：

1
2
3
4
5
6
7
8
9
10
// version 1: 暴力递归, 时间复杂度较高
public static int f1(int n) {
    if (n < 1) {
        return 0;
    }
    if (n == 1 || n == 2) {
        return 1;
    }
    return f1(n - 1) + f1(n - 2);
}

版本二：动态规划

可以使用滚动数组版本的动态规划解决该问题，但是其时间复杂度为 O(N)：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// version 2: 动态规划
public static int f2(int n) {
    if (n < 1) {
        return 0;
    }
    if (n == 1 || n == 2) {
        return 1;
    }
    int p = 0;
    int q = 1;
    int res = 0;
    // 注意i可以取到n
    for (int i = 2; i <= n; i++) {
        // f(n) = f(n-1) + f(n-2)
        res = p + q;
        // f(n-2) = f(n-1)
        p = q;
        // f(n-1) = f(n)
        q = res;
    }
    return res;
}

版本三：快速幂

可以使用矩阵的快速幂方法，其时间复杂度为 O(logN)

image-20211214221246265

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
// version 3: 快速幂
public static int f3(int  n) {
    if (n < 1) {
        return 0;
    }
    if (n == 1 || n == 2) {
        return 1;
    }
    int[][] base = new int[][]{{1, 1}, {1, 0}};
    int[][] res = matrixPower(base, n - 2);
    // f(n) = f(2) * res(0, 0) + f(1) * res(1, 0)
    return 1 * res[0][0] + 1 * res[1][0];
}

public static int[][] matrixPower(int[][] m, int p) {
    int[][] res = new int[m.length][m[0].length];
    // 矩阵对角线初始化为1
    for (int i = 0; i < m.length; i++) {
        res[i][i] = 1;
    }
    // 矩阵的一次方
    int[][] tmp = m;
    for (; p > 0; p >>= 1) {
        if ((p & 1) == 1) {
            res = matrixMulti(res, tmp);
        }
        tmp = matrixMulti(tmp, tmp);
    }
    return res;
}

private static int[][] matrixMulti(int[][] a, int[][] b) {
    // a * b 得到的维度是 a 的行 * b 的列
    int[][] res = new int[a.length][b[0].length];
    // 计算矩阵乘法结果
    for (int i = 0; i < a.length; i++) {
        for (int j = 0; j < b[0].length; j++) {
            // 计算对应行和列的元素累乘和
            for (int k = 0; k < a[0].length; k++) {
                res[i][j] += a[i][k] * b[k][j];
            }
        }
    }
    return res;
}

总结

快速幂的套路同样适合于严格递推关系的动态规划问题，比如本题的 f(n) = f(n - 1) + f(n - 2)，是一个严格递推关系，可以通过该关系枚举前几项构成方程组从而推算出 M 矩阵的具体值以及矩阵公式。西面再介绍几个可以使用该套路的题目。

递推过程：先枚举出前几项，构造方程组求解 a b c d 的值，即可求得 M：

image-20211215161354377

青蛙跳台阶

剑指 Offer 10- II. 青蛙跳台阶问题：一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

该问题与斐波那契数列非常相似，只是边界值不同而已：

  • 青蛙跳台阶问题： f(0)=1, f(1)=1, f(2)=2
  • 斐波那契数列问题： f(0)=0, f(1)=1, f(2)=1

该问题同样可以使用上面介绍的套路进行快速幂的计算，并且 M 矩阵也是相同的，唯一区别在于边界条件的值不相等。

母牛问题

一只母牛在出生三年后，每一年都可以开始生小牛，生出来的小牛在三年后也可以生小牛。假设母牛出生后永远不会死亡，则 n 年后总共有多少头牛？

该问题同样符合严格递推公式：f(n) = f(n - 1) + f(n - 3)。

其中 f(n - 1) 代表前一年存活的牛肯定也会活到第 n 年；f(n - 3) 代表三年前存活的母牛在第 n 年肯定都可以生育新的小牛，所以也要加上

image-20211215162519905

该问题若想采用快速幂进行求解时，可以构造成：f(n) = 1 * f(n - 1) + 0 * f(n - 2) + 1 * f(n - 3)。此时要构造的就是一个 3*3 的矩阵，有三次项：

image-20211215162724604

如果题目设定母牛会在 10 年后死亡，则该递推公式将改为：f(n) = f(n - 1) + f(n - 3) - f(n - 10)

把数字翻译成字符串

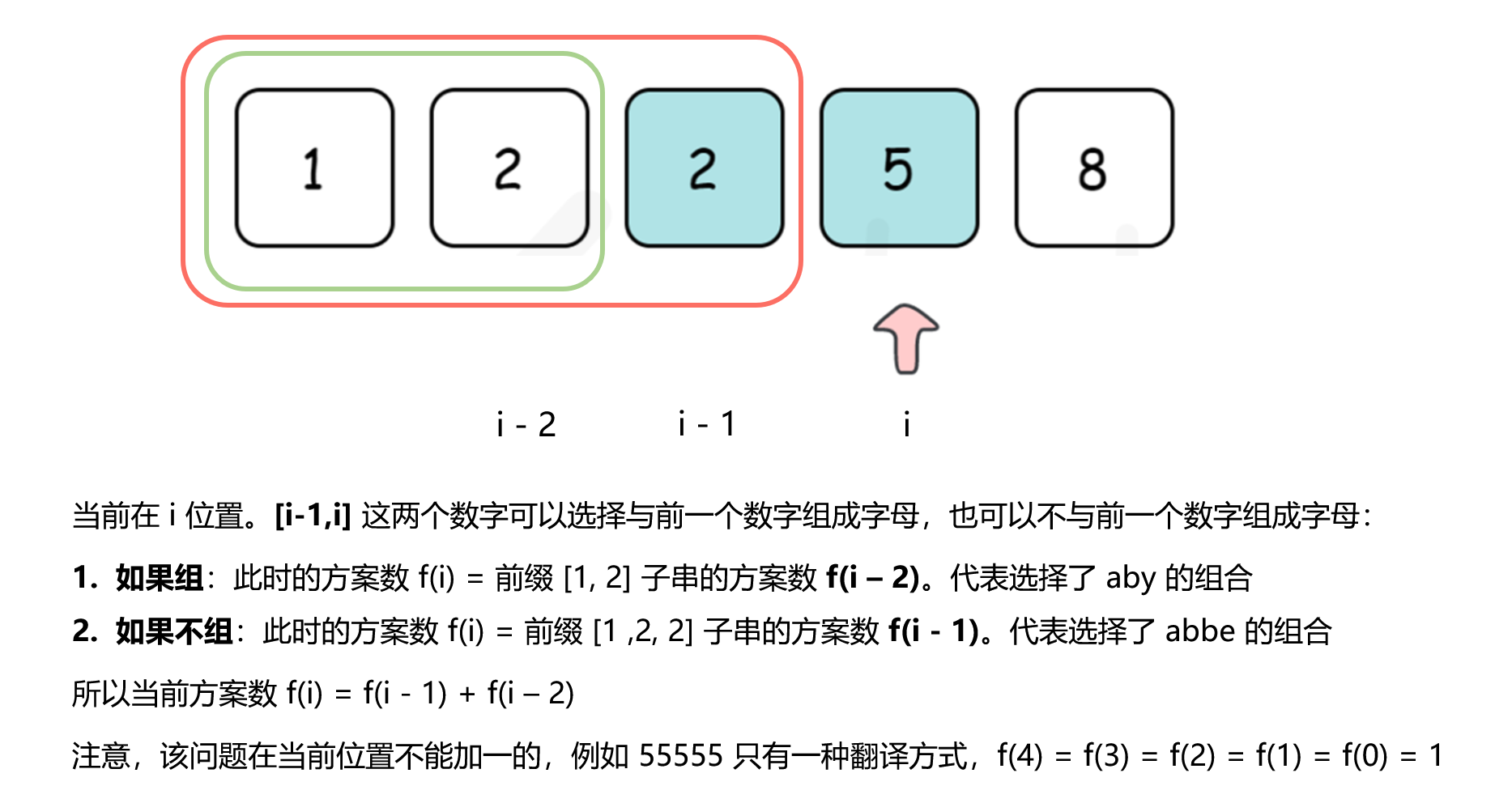
剑指 Offer 46. 把数字翻译成字符串：规定1和A对应、2和B对应、3和C对应…那么一个数字字符串比如"111"，就可以转化为"AAA"、“KA"和"AK”。给定一个只有数字字符组成的字符串str，返回有多少种转化结果。

思路：归纳出翻译的规则，字符串的第 i 位置：

  • 可以单独作为一位来翻译
  • 如果第 i - 1 位和第 i 位组成的数字在 10 到 25 之间，可以把这两位连起来翻译

记忆化递归尝试版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
public static List<String> convert(String str) {
    // 0. 如果到底，则开始将结果转换成String并加入到list中
    // 1. 当前数字为0，说明往后不能转换成字母，则递归栈开始返回，不会将当前分支转换成字符串
    // 2. 当前数字大于等于3，则只能将当前数字转换成字母，然后继续调用子问题
    // 3. 当前数字为1，有两种情况
    //   3.1 将当前数字转换为A，然后继续调用子问题
    //   3.2 不将当前数字进行转换，而是将其和下一位数字一起转换成一个英文字母（前提是下一位必须存在），然后继续调用子问题
    // 4. 当前数字为2，有两种情况
    //      4.1 将当前数字转换为B，然后继续调用子问题
    //      4.2 不将当前数字进行转换，而是将其和下一位数字一起转换成一个英文字母（前提是下一位必须存在且不大于6），然后继续调用子问题
    char[] arr = str.toCharArray();
    char[] tmp = new char[arr.length];
    List<String> res = new ArrayList<>();
    process(0, arr, tmp, res);
    return res;
}


public static void process(int i, char[] arr, char[] tmp, List<String> res) {
    if (i == arr.length) {
        // base case
        // 0. 如果到底，则开始将结果转换成String并加入到list中
        // 可以再加个处理，将为0的字符去掉不要
        res.add(new String(tmp));
        return;
    }

    // 1. 当前数字为0，说明往后不能转换成字母，则递归栈开始返回，不会将当前分支转换成字符串
    if (arr[i] == '0') {
        return;
    }
    // 2. 当前数字大于等于3，则只能将当前数字转换成字母，然后继续调用子问题
    if (arr[i] >= '3') {
        tmp[i] = (char)((int)'A' + (arr[i] - '1'));
        process(i + 1, arr, tmp, res);
        // i+1 层之后的都清空
        clearCache(tmp, i+1);
        return;
    }
    // 3. 当前数字为1，有两种情况
    if (arr[i] == '1') {
        // 3.1 将当前数字转换为A，然后继续调用子问题
        tmp[i] = 'A';
        process(i + 1, arr, tmp, res);
        // i+1 层之后的都清空，防止tmp后面的内容被其他分支修改，从而导致当前分支内容受影响
        clearCache(tmp, i+1);

        // 3.2 不将当前数字进行转换，而是将其和下一位数字一起转换成一个英文字母（前提是下一位必须存在）
        if (i + 1 < arr.length) {
            tmp[i] = (char)((int)'A' + (10 + arr[i + 1] - '1'));
            // 注意此时是从i+2调用子问题，因为i+1此时已经考虑进去了
            process(i + 2, arr, tmp, res);
            // i+1 层之后的都清空，防止tmp后面的内容被其他分支修改，从而导致当前分支内容受影响
            clearCache(tmp, i+1);
        }
        return;
    }
    // 4. 当前数字为2，有两种情况
    if (arr[i] == '2') {
        // 4.1 将当前数字转换为B，然后继续调用子问题
        tmp[i] = 'B';
        process(i + 1, arr, tmp, res);
        // i+1 层之后的都清空
        clearCache(tmp, i+1);

        // 4.2 不将当前数字进行转换，而是将其和下一位数字一起转换成一个英文字母（前提是下一位必须存在且不大于6），然后继续调用子问题
        if (i + 1 < arr.length && arr[i + 1] <= '6') {
            tmp[i] = (char) ((int) 'A' + (20 + arr[i + 1] - '1'));
            // 注意此时是从i+2调用子问题，因为i+1此时已经考虑进去了
            process(i + 2, arr, tmp, res);
            // i+1 层之后的都清空
            clearCache(tmp, i+1);
        }
    }
}

public static void clearCache(char[] tmp, int count) {
    for (int i = count; i < tmp.length; i++) {
        tmp[i] = '0';
    }
}

public static void main(String[] args) {
    System.out.println(convert("123"));
}

简化版问题：统计出可行的方案

当问题只需要统计出可行的方案时（不要求实际转换），条件 3 和 4 可以进行合并：如果当前位的数字和下一位的数字组成的数字处于 10 和 27 之间，则统一进行新一轮的递归。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static int process(char[] str, int index) {
    if (index == str.length) {
        return 1;
    }
    if (str[index] == '0') {
        return 0;
    }
    int res = process(str, index + 1);
    if (index == str.length - 1) {
        return res;
    }
    // 如果下一位还有并且在10到26之间，则可以将二者转换成一个字母
    if (((str[index] - '0') * 10 + str[index + 1] - '0') < 27) {
        res += process(str, index + 2);
    }
    return res;
}

动态规划版本

题解：https://leetcode-cn.com/problems/ba-shu-zi-fan-yi-cheng-zi-fu-chuan-lcof/solution/ba-shu-zi-fan-yi-cheng-zi-fu-chuan-by-leetcode-sol/

我们可以用 f(i) 表示以第 i 位结尾的前缀串翻译的方案数，考虑第 i 位单独翻译和与前一位连接起来再翻译对 f(i) 的贡献。

  • 单独翻译对 f(i) 的贡献为 f(i−1)；
  • 如果第 i - 1 位存在，并且第 i−1 位和第 i 位形成的数字 x 满足 10 ≤ x ≤ 25，那么就可以把第 i - 1 位和第 i 位连起来一起翻译，对 (i) 的贡献为 f(i−2)，否则为 0。

我们可以列出这样的动态规划转移方程：f(i)=f(i−1)+f(i−2)[i−1≥0,10≤x≤25]。边界条件是 f(-1) = 0，f(0) = 1。方程中 [c] 的意思是 c 为真的时候 [c] = 1，否则 [c] = 0。

image-20211210221236011

本质上是青蛙跳台阶问题

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public int translateNum(int num) {
    if (num < 0) {
        return 0;
    }
    String str = String.valueOf(num);
    int p = 1, q = 1, r = 1;
    String tmp = null;
    // 从 1 位置开始。1 位置的值 = -1 位置 + 0 位置，所以需要先设置 p 和 q 都是 1
    for (int i = 1; i < str.length(); i++) {
        r = p;
        tmp = str.substring(i - 1, i + 1);
        if (tmp.compareTo("10") >= 0 && tmp.compareTo("25") <= 0) {
            r += q;
        }
        // 更新 r p q
        q = p;
        p = r;
    }
    return r;
}

达标的字符串

给定一个数 N，想象只由 0 和 1 两种字符组成的所有长度为 N 的字符串。如果某个字符串任何 0 字符的左边都有 1 紧挨着，则认为这个字符串达标。返回有多少达标的字符串。

例如：

  • 达标的字符串：11101011101110
  • 不达标的字符串：001001000（只要有某个 0 的左边不是 1 就不达标）

思路：该问题同样是一道动态规划问题。可以进行以下尝试：

  • 如果当前位置设置为 1，则其没有额外限制，截至目前为止的种类数为 f(n) = f(n - 1)
  • 如果当前位置设置为 0，则其左边必须为 1，截至目前为止的种类数为 f(n) = f(n - 2)。因为 n-1 位置必须为 1，需要考虑前 n-2 的种类数

因此当前位置的总种类数为：f(n) = f(n - 1) + f(n - 2)。

该问题与“把数字翻译成字符串”问题类似，本质上都是青蛙跳台阶问题

注意：要从 1 开始遍历，因为 0 位置必须为 “1”

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
// 动态规划版本
public static int getNum1(int n) {
    if (n < 1) {
        return 0;
    }
    if (n == 1) {
        return 1;
    }
    int pre = 1;
    int cur = 1;
    int tmp = 0;
    // 要从 1 开始遍历，因为 0 位置必须为 "1"
    // 遍历 n - 1 次（取出首位必须为 1 的情况）
    for (int i = 2; i <= n; i++) {
        tmp = cur;
        cur += pre;
        pre = tmp;
    }
    return cur;
}

// 递归版本
public static int getNum2(int n) {
    if (n < 1) {
        return 0;
    }
    return process(1, n);
}
public static int process(int i, int n) {
    if (i == n - 1) {
        return 2;
    }
    if (i == n) {
        return 1;
    }
    return process(i + 1, n) + process(i + 2, n);
}

// 快速幂版本
public static int getNum3(int n) {
    if (n < 1) {
        return 0;
    }
    if (n == 1 || n == 2) {
        return n;
    }
    int[][] base = { { 1, 1 }, { 1, 0 } };
    int[][] res = matrixPower(base, n - 2);
    return 2 * res[0][0] + res[1][0];
}

public static int[][] matrixPower(int[][] m, int p) {
    int[][] res = new int[m.length][m[0].length];
    for (int i = 0; i < res.length; i++) {
        res[i][i] = 1;
    }
    int[][] tmp = m;
    for (; p != 0; p >>= 1) {
        if ((p & 1) != 0) {
            res = muliMatrix(res, tmp);
        }
        tmp = muliMatrix(tmp, tmp);
    }
    return res;
}

public static int[][] muliMatrix(int[][] m1, int[][] m2) {
    int[][] res = new int[m1.length][m2[0].length];
    for (int i = 0; i < m1.length; i++) {
        for (int j = 0; j < m2[0].length; j++) {
            for (int k = 0; k < m2.length; k++) {
                res[i][j] += m1[i][k] * m2[k][j];
            }
        }
    }
    return res;
}

铺瓷砖

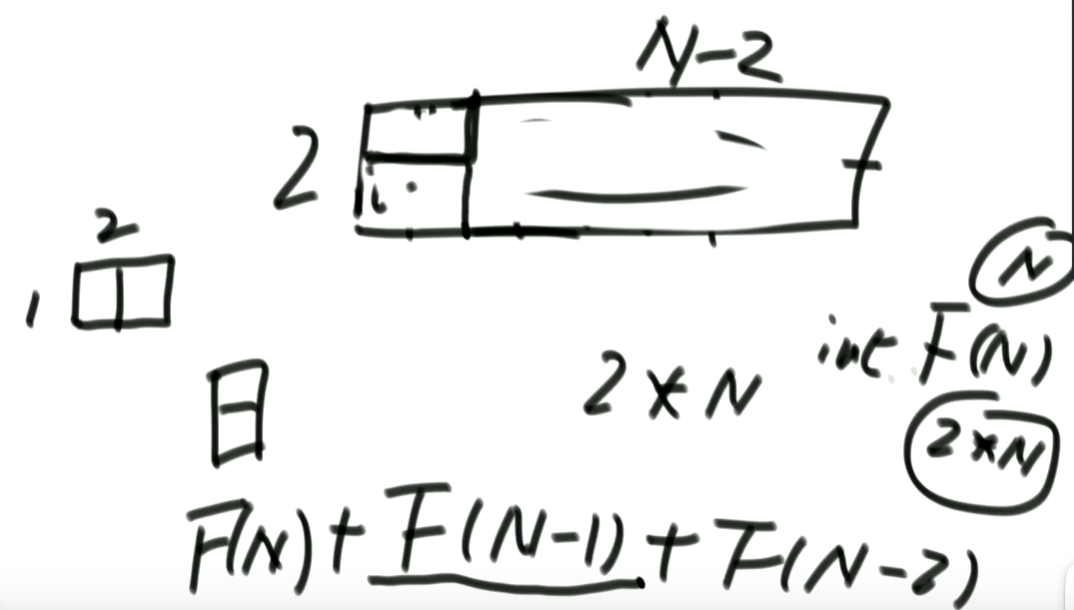
假设有一个 2*N 面积的地面，我们有足够多数量的瓷砖（尺寸为 1 * 2 或 2 * 1），则完全铺满该地面有多少种铺法。

思路：该问题的本质同样是青蛙跳台阶。当前位置的尝试方法：

  • 如果上一个瓷砖是 1 * 2 尺寸，则当前位置也必须是 1 * 2 尺寸。此时的铺法为 f(n - 2)。因为1 * 2 的尺寸占用了两个单元，所以要减二
  • 如果上一个瓷砖是 2 * 1 尺寸，则当前位置也必须是 2 * 1 尺寸。此时的铺法为 f(n - 1)。因为2 * 1 的尺寸占用了一个单元，所以要减一

所以总的铺法就是f(n) = f(n - 1) + f(n - 2)。

image-20211215164225152

打家劫舍系列问题

打家劫舍 I

198. 打家劫舍：你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

方法一：记忆化搜索版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public int rob(int[] nums) {
    if (nums == null || nums.length == 0) {
        return 0;
    }
    int[] record = new int[nums.length];
    for (int i = 0; i < record.length; i++) {
        record[i] = -1;
    }
    return recur(nums, 0, record);
}

public int recur(int[] nums, int i, int[] record) {
    // 上一次递归偷了倒数第三家，此时就可以偷倒数第一家
    if (i == nums.length - 1) {
        return nums[nums.length - 1];
    }
    // 上一次递归偷了倒数第二家，那么此时就没得偷了
    if (i == nums.length) {
        return 0;
    }
    // 记忆化搜索
    if (record[i] != -1) {
        return record[i];
    }

    // 当前位置 i 偷与不偷的最大值
    record[i] = Math.max(
        recur(nums, i + 1, record),
        recur(nums, i + 2, record) + nums[i]
    );
    return record[i]; 
}

方法二：动态规划版本，使用三个变量 p，q，r（注意p的初始值是二者的最大值，而不是nums[1]）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 使用三个变量：p, q, r
public int rob(int[] nums) {
    if (nums == null) {
        return 0;
    }
    if (nums.length == 1) {
        return nums[0];
    } else if (nums.length == 2) {
        return Math.max(nums[0], nums[1]);
    }

    int p = nums[0];
    // 注意 p 的初始值是二者的最大值，而不是 nums[1]
    int q = Math.max(nums[1], nums[0]);
    int r = 0;
    for (int i = 2; i < nums.length; i++) {
        r = Math.max(p + nums[i], q);
        p = q;
        q = r;
    }
    return r;
}

方法三：动态规划版本，使用两个变量 p，q，r

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 使用两个变量：p, q
public int rob(int[] nums) {
    if (nums == null) {
        return 0;
    }
    if (nums.length == 1) {
        return nums[0];
    }

    int p = nums[0];
    // 注意 p 的初始值是二者的最大值，而不是 nums[1]
    int q = Math.max(nums[1], nums[0]);
    for (int i = 2; i < nums.length; i++) {
        int tmp = q;
        q = Math.max(p + nums[i], q);
        p = tmp;
    }
    return q;
}

打家劫舍 II

213. 打家劫舍 II：你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。

给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金额。

思路：环状排列意味着第一个房子和最后一个房子中只能选择一个偷窃，因此可以把此环状排列房间问题约化为两个单排排列房间子问题：

  • 偷第一家，则计算偷 [0, n -1] 家的最大金额
  • 不偷第一家（代表可能偷最后一家），然后计算偷 [1, n] 家的最大金额

最后求二者的最大值即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public int rob(int[] nums) {
    if(nums.length == 0) return 0;
    if(nums.length == 1) return nums[0];
    return Math.max(myRob(Arrays.copyOfRange(nums, 0, nums.length - 1)), 
                    myRob(Arrays.copyOfRange(nums, 1, nums.length)));
}

private int myRob(int[] nums) {
    int pre = 0, cur = 0, tmp;
    for(int num : nums) {
        tmp = cur;
        cur = Math.max(pre + num, cur);
        pre = tmp;
    }
    return cur;
}

打家劫舍 III

股票系列问题

买卖股票的最佳时机

假设把某股票的价格按照时间先后顺序存储在数组中，请问买卖该股票一次可能获得的最大利润是多少？

思想：遍历每个元素，规定必须在当前元素卖出的情况下，在其前面哪个地方买，收益最大

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public int maxProfit(int[] prices) {
    if (prices == null || prices.length < 1) {
        return 0;
    }
    int ans = 0;
    // 最小值初始化为第一个值
    int min = prices[0];

    // 思想是：遍历每个元素，规定当前元素必须卖出的情况下，在其前面哪个地方买，收益最大
    for (int i = 1; i < prices.length; i++) {
        // 先更新当前区间内的最小值
        min = Math.min(prices[i], min);
        // 然后更新当前区间内卖出的最大收益
        // 1. 如果当前值小于当前区间内的最小值，则说明当前区间卖出得到的是负收益，那么其再与ans取最大值，就会得到前面位置的最大值，意味着当前得不到更大的值，不更新ans
        // 2. 如果当前值大于当前区间内的最大值，则如果当前点必须卖出的话，得到的最大收益就是当前值-min
        ans = Math.max(prices[i] - min, ans);
    }
    return ans;
}

买卖股票的最佳时机 II

给定一个数组 prices ，其中 prices[i] 是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

思路：任意次数的购买，最佳策略就是记录所有上升的区间的收益。将整体进行离散化考虑，对每个上升的子区间都进行累加收益，代表只要发现有收益，就进行一笔买卖，累加收益。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public int maxProfit(int[] prices) {
    // 任意次数的购买，最佳策略就是记录所有上升的区间的收益
    // 在代码中的较好实现方式为：
    // 从index == 1 位置开始遍历数组：
    //   1. 如果当前价格大于前一个价格，说明前一个位置买，当前位置卖可以得到一笔收益，因此更新总收益。表示在前一个位置买，当前位置全卖
    //   2. 如果当前价格小于等于前一个价格，说明前一个买，当前位置卖无法得到一笔收益，因此不更新总收益，表示不买不卖
    // 整体的思想是，判断当前位置是否比前一个位置价格高
    // 如果高，就前一个位置买，当前位置全卖，完成一笔交易，更新收益
    // 如果不高，就不做任何交易，不更新收益
    // 整个过程不需要额外一个min记录最小值，因为每笔交易都是立即成交，立即更新的，之前买过的位置不会再买一次

    int ans = 0;
    // 注意要从1开始
    for (int i = 1; i < prices.length; i++) {
        //  不需要更新当前区间的最小值，交易和更新是实时的
        if (prices[i] > prices[i - 1]) {
            ans += prices[i] - prices[i - 1];
        }
    }    
    return ans;  
}

买卖股票的最佳时机 III

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成两笔交易。注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

整体思想：将在当前区间内买两次拆成两个步骤：

  • 先在当前区间内买卖一次，并必须在当前区间内买一笔，并且令二者的总收益最大，这样后面再在当前点卖就肯定能获得最大收益；
  • 第二次遍历所有位置，在每个当前位置卖出，即可得到在当前区间内买卖两笔的总收益

那么遍历完所有位置，肯定能得到全局最大的收益值。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public int maxProfit(int[] prices) {
    if (prices == null || prices.length < 2) {
        return 0;
    }
    // 1. doneOnceMax: [0, i] 区间内只卖卖一次，获得的最大收益。注意这里卖出的时机不要求是当前位置，而是这个区间任意位置均可以
    int[] doneOnceMax = new int[prices.length];
    // 0 位置的收益肯定是0.
    doneOnceMax[0] = 0;
    int min = prices[0];

    for (int i = 1; i < prices.length; i++) {
        // 先保存当前区间的最小值
        min = Math.min(min, prices[i]);
        // 注意这里要和前一个位置比较，如果更大就保存，否则就保存前一个的值
        doneOnceMax[i] = Math.max(prices[i] - min, doneOnceMax[i - 1]); 
    }

    // 整体思想就是，将买两次拆成两个步骤：
    // 1. 买卖一次，并必须在当前区间内买一笔，让总收益最大，这样后面再卖就肯定能获得最大收益
    // 2. 再在当前位置卖出，
    // 那么遍历所有位置，肯定能得到最大的收益值

    // 2. 然后计算 doneOnceMinusOneBuyMax：代表[0, i]区间上任意位置买卖一笔，然后再买一笔后的最大收益
    // 要达到最大，就要先完成一笔比较好的收益，然后再买一个价格便宜的位置
    int[] doneOnceMinusOneBuyMax = new int[prices.length];
    // doneOnceMinusOneBuyMax[0]：买卖一笔还得再买一笔，那收益肯定是 -prices[0]
    doneOnceMinusOneBuyMax[0] = -1 * prices[0];
    // 从 1 位置开始遍历
    for (int i = 1; i < prices.length; i++) {
        // 两种情况取最大：
        // 1. 不在当前点买入一笔，那么当前位置区间的值肯定等于[0, i-1]区间内的值
        // 2. 在当前点卖买入一笔，那么当前区间内的值等于该区间内只卖卖一次的最大收益（doneOnceMax[i]）- 当前价格（prices[i]）
        doneOnceMinusOneBuyMax[i] = Math.max(doneOnceMinusOneBuyMax[i - 1], doneOnceMax[i] - prices[i]);
    }

    // 3. 在遍历每个元素，doneOnceMinusOneBuyMax + 当前price，即可得到[0, i]区间内的最大收益
    // 思想：在前面买卖了一笔，又买了一笔便宜的，这样再在当前位置卖（必须在当前位置卖，思路同股票I中的卖的规定），那么遍历所有的情况取最大值，就是答案了
    int ans = 0;
    for (int i = 0; i < prices.length; i++) {
        ans = Math.max(doneOnceMinusOneBuyMax[i] + prices[i], ans);
    }

    return ans;
}

左右括号系列问题

合法括号匹配序列的深度

一个合法的括号匹配序列有以下定义：

  • 空串 “” 是一个合法的括号匹配序列
  • 如果 “X” 和 “Y” 都是合法的括号匹配序列，“XY” 也是一个合法的括号匹配序列
  • 如果 “X” 是一个合法的括号匹配序列，那么 “(X)” 也是一个合法的括号匹配序列
  • 每个合法的括号序列都可以由以上规则生成。

例如：""，"()"，"()()"，"((()))" 都是合法的括号序列。对于一个合法的括号序列我们又有以下定义它的深度:

  • 空串 “” 的深度是0
  • 如果字符串 “X” 的深度是 x，字符串 “Y” 的深度是y，那么字符串 “XY” 的深度为 max(x,y)
  • 如果 “X” 的深度是 x，那么字符串 “(X)” 的深度是 x+1

例如："()()()" 的深度是 1，"((()))" 的深度是 3。现在给你一个合法的括号序列，需要你计算出其深度。

思路：定义变量 count，遍历字符串：

  • 当遇到左括号时，count++，代表当前子序列的深度加一；
  • 当 count 等于 0 时，说明已经经过了某一个合法的括号子序列，记录此时的 count 到结果中（取最大值）
  • 遍历完整个字符串后，即可得到最大的深度

代码：

1
// 未来补充

括号序列合法化

给定义一个可能不合法的括号序列，求至少需要添加多少个括号才能令该括号序列变得合法。

思路：定义变量 count 记录左右括号出现的情况，定义 ans 记录需要添加的括号数量，遍历字符串：

  • 如果遇到左括号，则 count++
  • 如果遇到右括号，则先判断 count 此时是否是 0
    • 如果是，则代表当前的右括号在左侧没有匹配的左括号，需要添加一个左括号，ans++
    • 如果不是，则还不需要添加左括号，count–

遍历完毕后，count 的数量就是没有匹配的左括号的数量，ans 的数量就是没有匹配的右括号的数量，二者相加即是答案。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public class NeedParentheses {
    public static int needParentheses(String s) {
        // 遍历过程中记录当前左右括号出现情况
        int count = 0;
        int ans = 0;
        for (int i = 0; i < s.length(); i++) {
            // 如果是 (, 则count++
            if (s.charAt(i) == '(') {
                count++;
            } else if (s.charAt(i) == ')') {
                // 如果是 ), 则先判断count此时是否是0,
                if (count == 0) {
                    // 如果是, 代表当前的 ) 在左侧没有匹配的 (, ans++
                    ans++;
                    // 不需要再额外count--了
                } else {
                    count--;
                }
            }
        }
        // 出循环时, count 的数量就是没有匹配的 ( 的数量, ans 的数量就是没有匹配的 ) 的数量
        return ans + count;
    }

    public static void main(String[] args) {
        System.out.println(needParentheses("Sadadsd)dsd(((dsds))"));
    }
}

最长有效括号

32. 最长有效括号：给你一个只包含 '(' 和 ')' 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

方法一：双指针 + 双向遍历

本质上是一种贪心策略

在此方法中，我们利用两个计数器 left 和 right。首先，我们从左到右遍历字符串，对于遇到的每个 左括号，我们增加 left 计数器，对于遇到的每个右括号，我们增加 right 计数器。每当 left 计数器与 right 计数器相等时，我们计算当前有效字符串的长度，并且记录目前为止找到的最长子字符串。当 right 计数器比 left 计数器大时，我们将 left 和 right 计数器同时变回 0。

这样的做法贪心地考虑了以当前字符下标结尾的有效括号长度，每次当右括号数量多于左括号数量的时候之前的字符我们都扔掉不再考虑，重新从下一个字符开始计算，但这样会漏掉一种情况，就是遍历的时候左括号的数量始终大于右括号的数量，即 (() ，这种时候最长有效括号是求不出来的。

解决的方法也很简单，我们只需要从右往左遍历用类似的方法计算即可，只是这个时候判断条件反了过来：

  • 当 left 计数器比 right 计数器大时，我们将 left 和 right 计数器同时变回 0
  • 当 left 计数器与 right 计数器相等时，我们计算当前有效字符串的长度，并且记录目前为止找到的最长子字符串

思路总结：

  • 一旦相等，就找到了一个局部的有效子串，更新长度，然后遍历（注意此时可不能令 left 和 right 归零，因为其后面可能还连着更长的有效子串）
  • 如果一直是右括号（体现在 right > left），则不可能是有效的，那么算法就会一直令 left 和 right 清零，代表这些右括号开头的子串不可能有效
  • 如果先是左括号，则 left > right，不会清空，继续遍历，直到 right == left，代表之前的左括号都找到了对应的匹配右括号，那么就进行更新，然后继续遍历。
  • 直到 right > left，代表当前有效子串后面多加了一个右括号，导致当前子串不是有效的了，那么就二者一起清零，开始判断当前位置的下一个位置往后还有没有有效的（这里很重要的思想就是：一旦 right > left，那么 [left, right] 区间内任意位置开头的子串都不可能再和后面的子串拼接起来了（因为当前位置的右括号始终补不上），所以才会直接令 left 和 right 清零，表示不再考虑刚才的子串了，重新开始，这也就避免了重复遍历数组，使得时间复杂度为 O(N)）

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// 双指针从前往后遍历 + 从后往前遍历
public int longestValidParentheses02(String s) {
    int left = 0, right = 0, maxlength = 0;
    // 正向遍历：如果遇到左括号 left 就右移，否则 right 移动
    // 每到一个位置，就判断此时的 left 是否等于 right，
    // 1. 如果相等则找到了一个有效的子串，更新长度 2 * right
    // 2. 如果 right > left，则此时说明当前子序列的右括号比左括号多，那肯定不是有效的，舍弃掉 
    for (int i = 0; i < s.length(); i++) {
        if (s.charAt(i) == '(') {
            left++;
        } else {
            right++;
        }
        if (left == right) {
            maxlength = Math.max(maxlength, 2 * right);
        } else if (right > left) {
            left = right = 0;
        }
    }
    left = right = 0;
    // 再反向遍历一遍，操作相反，思想一致
    for (int i = s.length() - 1; i >= 0; i--) {
        if (s.charAt(i) == '(') {
            left++;
        } else {
            right++;
        }
        if (left == right) {
            maxlength = Math.max(maxlength, 2 * left);
        } else if (left > right) {
            left = right = 0;
        }
    }
    return maxlength;
}

方法二：动态规划

https://www.bilibili.com/video/BV13g41157hK?p=21

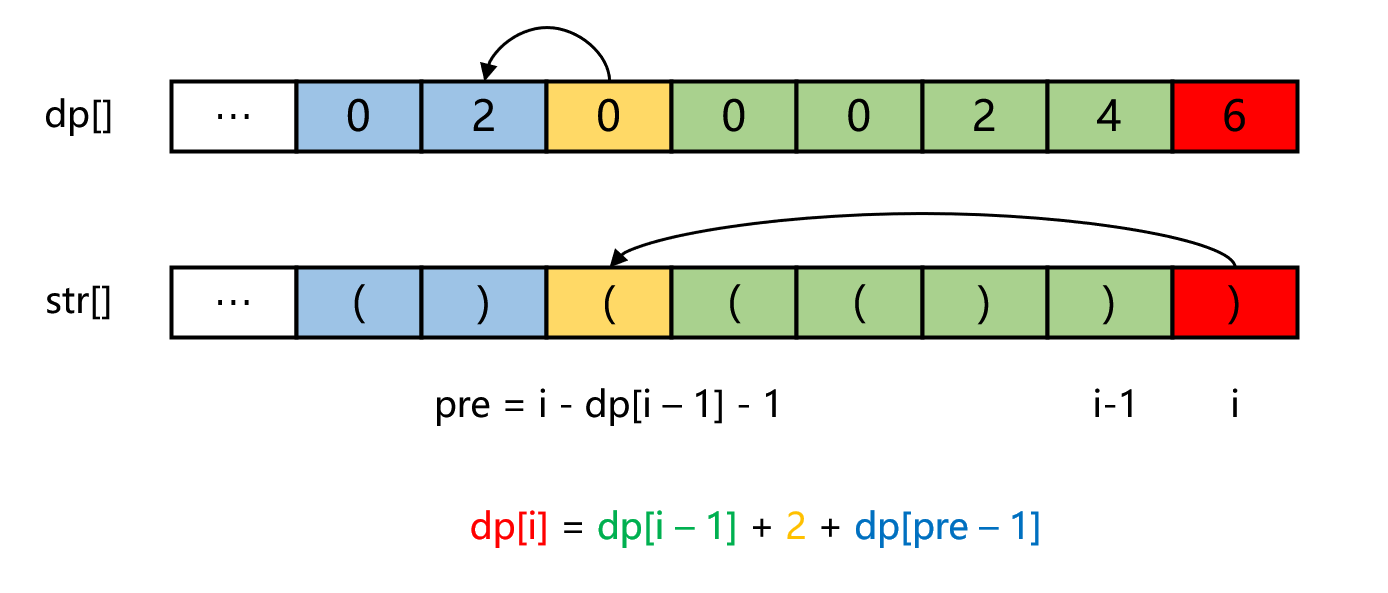
思想：计算出以每个位置作为有效字符串的结尾时，当前子字符串的长度，取最大值即可得到答案。当前位置能作为有效字符串的结尾的前提是：当前位置必须是左括号，如果是右括号，肯定不能作为结尾。

  • 令 pre 指向 dp[i-1]，代表的合格子串的前一个位置（见下图的黄色块）
  • 判断 pre 位置的符号是否为 (：
    • 如果是，则恰好能和当前 i 的 ) 组成一个 ( (...dp[i-1]...) ) 合格子串（见下图的黄色块 + 绿色块 + 红色块）
      • 如果 pre-1 位置 dp[pre - 1] 不为 0，则将其也纳入当前的子串（见下图的蓝色块），否则长度就是 dp[i-1] 的长度 + 2
    • 如果是 )，则不能和当前的 ）构成合格子串，则当前位置的 dp[i] 值为 0

示意图：

image-20211218210931962

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
    public int longestValidParentheses(String s) {
        if (s == null || s.length() < 1) {
            return 0;
        }
        return longestValidParentheses03(s);
    }

    // 动态规划：计算出以每个位置作为有效字符串的结尾时，当前子字符串的长度，取最大值即可得到答案
    // 当前位置能作为有效字符串的结尾的前提是：当前位置必须是)，如果是(，肯定不能作为结尾
    public int longestValidParentheses03(String s) {
        int[] dp = new int[s.length()];
        char[] str = s.toCharArray();
        int pre = 0;
        int res = 0;
        // dp[0] = 0，只需要从1开始遍历
        for (int i = 1; i < s.length(); i++) {
            // 如果为(，则当前位置肯定不能作为字符串的结尾，dp值设置为0
            if (str[i] == '(') {
                dp[i] = 0;
                continue;
            } else {
                // 如果当前位置为)，则可以作为结尾。
                // pre 指向dp[i-1]代表的合格子串的前一个位置符号
                pre = i - dp[i - 1] - 1;
                // 判断该位置的符号是否为(，如果是，则恰好能和当前i的)组成一个( (...dp[i-1]...) )合格子串
                if (pre >= 0 && str[pre] == '(') {
                    // 如果pre-1还有，则将其也纳入当前的子串
                    // 否则长度就是 dp[i-1]的长度 + 2
                    dp[i] = pre - 1 >=0 ? dp[i - 1] + 2 + dp[pre - 1] : dp[i - 1] + 2;
                } else {
                    // 如果是)，则i位置的最长合格子串是0
                    dp[i] = 0;
                }

            }
            res = Math.max(res, dp[i]);
        }
        return res;
    }

   
}