【算法】贪心算法

发表于2021-11-28更新于2022-03-02字数统计9.1k阅读时长62分阅读次数

贪心算法常见题目

把数组排成最小的数

剑指 Offer 45. 把数组排成最小的数：输入一个非负整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。

贪心策略：若拼接字符串 x + y > y + x，则 x “大于” y ；反之，若 x + y < y + x ，则 x “小于” y。

x “小于” y 代表：排序完成后，数组中 x 应在 y 左边；“大于” 则反之。

根据以上规则，套用任何排序方法对 nums 执行排序即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
public String minNumber(int[] nums) {
    String[] strs = new String[nums.length];
    for(int i = 0; i < nums.length; i++)
        strs[i] = String.valueOf(nums[i]);
    // 自定义比较器
    Arrays.sort(strs, (x, y) -> (x + y).compareTo(y + x));
    StringBuilder res = new StringBuilder();
    for(String s : strs)
        res.append(s);
    return res.toString();
}

会议室问题

一些项目要占用一个会议室宣讲，会议室不能同时容纳两个项目的宣讲。 给你每一个项目开始的时间和结束的时间（给你一个数组，里面是一个个具体的项目），你来安排宣讲的日程，要求会议室进行的宣讲的场次最多。 返回这个最多的宣讲场次。

贪心策略：按照结束时间从小到大排序，优先选择结束时间更小的会议。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int intervalIntersection(int[][] programs) {
    // 按照结束时间排序
    Arrays.sort(programs, (o1, o2) -> o1[1] - o2[1]);
    int count = 0;
    int curTime = 0;
    for (int i = 0; i < programs.length; i++) {
        // 如果当前时间小于开始时间
        if (curTime <= programs[i][0]) {
            count++;
            // 更新当前时间
            curTime = programs[i][1];
        }
    }
    return count;
}

小虎买苹果

方法一：普通贪心策略——先尽可能多的买 8个的袋子

  • 如果要买的苹果数量是奇数，则没有答案，直接返回 -1。
  • 如果要买的苹果是偶数，则开始贪心：
    • 先尽可能多的买 8 个的袋子，判断此时剩余的苹果能不能被 6 整除，如果可以找到了最佳方案。
    • 如果不行，减少一个 8个的袋子，再看剩余的苹果能不能被 6 整除。
    • 重复该过程直到 8个的袋子为 0，如果剩余的苹果还不能被 6 整除，则说明没有满足条件的装法。

这种贪心策略会优先考虑买 8个的袋子，从而能保证得到的结果是最优的。

方法一的优化版本

可以对方法一进行优化：当剩余的苹果数量大于 24 时不需要再往下尝试了，后续不可能在存在可行方案了。这里的 24 是 6 和 8 的最小公倍数。如果该数字能被 6 整除，则其肯定能被 8 整除。但是在上面的尝试中已经表明了该数字不能被 8 整除，否则也不会遍历到当前位置。因此这个数字肯定也不能被 6 整除。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
public class AppleMinBags {
    public static int minBags(int n) {
        // 小于 6 个肯定不可行
        if (n <= 5) {
            return -1;
        }
        // 如果 n 为奇数, 肯定也不可行
        if (n % 2 == 1) {
            return -1;
        }
        /*
         * 贪心策略: 先尝试 8个的袋子, 如果剩余的无法被 6 整除, 再减去一个 8个的袋子, 继续尝试
         * 如果尝试到发现剩余的苹果数量大于 24( 8 和 6 的最小公倍数), 则不可能有可行方案, 直接返回
         */
        int bag8 = n / 8;
        // 初始化为 -1, 这样在遍历完毕后判断 bag6 是否为 -1, 如果是则不存在可行方案
        int bag6 = -1;
        int rest = n - bag8 * 8;
        while (bag8 >= 0 && rest < 24) {
            // 判断当前剩余的苹果能否被 6 整除
            bag6 = minBagBase6(rest);
            if (bag6 != -1) {
                break;
            }
            // 减少一袋, 继续尝试
            bag8--;
            rest = n - bag8 * 8;
        }
        return bag6 != -1 ? bag6 + bag8 : -1;
    }

    public static int minBagBase6(int n) {
        // 如果能整除就返回数量, 否则返回 -1
        return (n % 6 == 0) ? n / 6 : -1;
    }

    // 打表:
    public static int minBagAwesome(int apple) {
        if ((apple & 1) != 0) {
            return -1;
        }
        if (apple < 18) {
            return apple == 0 ? 0 : (apple == 6 || apple == 8) ? 1
                : (apple == 12 || apple == 14 || apple == 16) ? 2 : -1;
        }
        return (apple - 18) / 8 + 3;
    }

    public static void main(String[] args) {
        int max = Integer.MAX_VALUE;
        int testTime = 100000000;
        for (int test = 0; test < testTime; test++) {
            int apple = (int) (Math.random() * max);
            if (minBags(apple) != minBagAwesome(apple)) {
                System.out.println("error");
            }
        }

    }
}

避免洪水泛滥

1488. 避免洪水泛滥：你的国家有无数个湖泊，所有湖泊一开始都是空的。当第 n 个湖泊下雨的时候，如果第 n 个湖泊是空的，那么它就会装满水，否则这个湖泊会发生洪水。你的目标是避免任意一个湖泊发生洪水。

给你一个整数数组 rains ，其中：

  • rains[i] > 0 表示第 i 天时，第 rains[i] 个湖泊会下雨。
  • rains[i] == 0 表示第 i 天没有湖泊会下雨，你可以选择 一个湖泊并抽干这个湖泊的水。

请返回一个数组 ans ，满足：

  • ans.length == rains.length
  • 如果 rains[i] > 0 ，那么 ans[i] == -1。
  • 如果 rains[i] == 0，ans[i] 是你第 i 天选择抽干的湖泊。

如果有多种可行解，请返回它们中的 任意一个 。如果没办法阻止洪水，请返回一个 空的数组 。

https://leetcode-cn.com/problems/avoid-flood-in-the-city/solution/avoid-flood-in-the-city-by-ikaruga/、https://leetcode-cn.com/problems/avoid-flood-in-the-city/solution/java-hashmap-hashset-treeset-mian-xiang-vxeda/

思路：

  • 将晴天的日期全部记录到 TreeSet 中
  • 使用 HashMap 来记录每个湖泊上一次下雨的日期
  • 遇到晴天时先不用管抽哪个湖
  • 当下雨时，湖泊已经水满了时，我们可以查询到上次下雨的日期
  • 通过这个日期在晴天记录中查找对应的晴天日期。在有序数据中使用二分查找
  • 如果找到了，就可以使用那一天抽水，找不到就不可避免的洪水了。找到了更新下雨表中当前湖泊的日期为当前日期。

其中：

  • 核心思想 ： 遇到可以抽水的天时，把它存起来，遇到满水湖泊需要抽水时，观察上次该湖泊满水时与当前日期之间是否有可抽水天气 ， 取最靠近上次满水的那一个晴天。
  • HashMap 作用 ：记录某湖泊最近一次蓄满水的日期（同一时刻某个湖泊只会存一个日期，当遇到同一湖泊的另一个下雨日期时，就要进行处理，处理完毕后更新该湖泊的下雨日期为当前日期）。
  • TreeSet 作用 ：存晴天日期，用于二分查找出对某需要抽水湖泊的最佳抽水日期（距离该湖泊上一次下雨的最近日期）。
  • 空闲的晴天 ：设为1。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
public int[] avoidFlood(int[] rains) {
    if (rains == null || rains.length < 1) {
        return rains;
    }

    // 使用有序树保存晴天，使用 set.higher(i) 方法能返回比 i 大的最小元素，也就是比 i 大的距离他最近的元素
    TreeSet<Integer> sunnyDaySet = new TreeSet<>();
    // 使用哈希表保存下雨天的湖泊编号以及其索引。key：湖泊编码，value：该湖泊下雨天的索引
    HashMap<Integer, Integer> rainyDayMap = new HashMap<>();
    int[] res = new int[rains.length];
    // 按照题意初始化
    Arrays.fill(res, -1);

    for (int i = 0; i < rains.length; i++) {
        if (rains[i] == 0) {
            // 如果当前天是晴天，则加入到有序表中
            sunnyDaySet.add(i);
            // 按照题意，晴天如果不抽水，则设置为 1
            res[i] = 1;
            continue;
        }
        if (!rainyDayMap.containsKey(rains[i])) {
            // 如果下雨表中没保存过当前湖泊编号，则说明该湖泊还没下过雨，将其添加到表中
            rainyDayMap.put(rains[i], i);
            continue;
        }
        /* 如果当前天是下雨天，且已经存在于下雨表中，则需要从晴天表里选出某一天来清空当前下雨的湖泊。
            * 并且要选出的这一天需要是距离该湖泊上一次下雨后最近的一个晴天
            * 也就是在晴天表中比该湖泊上一次下雨天要大的天数中最小的一个，使用 higher() 方法可以实现（二分查找）
            */
        Integer recentDay = sunnyDaySet.higher(rainyDayMap.get(rains[i]));
        if (recentDay == null) {
            // 如果找不到，则返回
            return new int[0];
        }
        // 如果找得到，就修改 res 中该晴天锁抽干的湖泊编号，并从晴天表中删掉该天
        res[recentDay] = rains[i];
        // 注意！！！当前日期变更为该湖泊的最近满水日期，要记得更新当前湖泊的下雨天
        rainyDayMap.put(rains[i] , i);
        sunnyDaySet.remove(recentDay);
    }
    return res;
}

课程表 III

630. 课程表 III：这里有 n 门不同的在线课程，按从 1 到 n 编号。给你一个数组 courses ，其中 courses[i] = [durationi, lastDayi] 表示第 i 门课将会持续上 durationi天课，并且必须在不晚于 lastDayi 的时候完成。你的学期从第 1 天开始。且不能同时修读两门及两门以上的课程。返回你最多可以修读的课程数目。

贪心策略：对于两门课，如果后者的关闭时间较晚 ，那么我们先学习前者，再学习后者，总是最优的。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public int scheduleCourse(int[][] courses) {
    // 以结束时间排序
    Arrays.sort(courses, (c1, c2) -> c1[1] - c2[1]);
    // 储存已选择的课程，按照持续时间降序排序
    PriorityQueue<int[]> heap = new PriorityQueue<>((c1, c2) -> c2[0] - c1[0]);
    int day = 0;
    for (int[] c : courses) {
        if (day + c[0] <= c[1]) {
            // 如果当前课程时间不冲突，将该课程加入队列
            // 这里的不冲突可以理解为，0~day+c[0]这段区间，我们还可以再插入当前一节课
            day += c[0];
            heap.offer(c);
        } else if (!heap.isEmpty() && heap.peek()[0] > c[0]) {
            // 课程时间冲突，且有选过其他课，这时我们找到最长时间的课程，用当前的短课替换了，余出了更多的空区间
            // 所以这里我们余出的时间其实就是两者的持续时间之差，课程变短了，day会前移，这样我们相当于变相给后面的课程增加了选择的区间
            day -= heap.poll()[0] - c[0];
            heap.offer(c);
        }
    }
    return heap.size();
}

超级洗衣机

517. 超级洗衣机：假设有 n 台超级洗衣机放在同一排上。开始的时候，每台洗衣机内可能有一定量的衣服，也可能是空的。在每一步操作中，你可以选择任意 m (1 <= m <= n) 台洗衣机，与此同时将每台洗衣机的一件衣服送到相邻的一台洗衣机。

给定一个整数数组 machines 代表从左至右每台洗衣机中的衣物数量，请给出能让所有洗衣机中剩下的衣物的数量相等的最少的操作步数 。如果不能使每台洗衣机中衣物的数量相等，则返回 -1 。

思路：遍历每一个位置，判断当前位置 i 的左侧一共需要多少件衣服（需要拥有的 - 实际拥有的）：

  • 该值如果大于 0，说明实际拥有的比较少，需要当前位置以及右侧给其输入衣服
  • 该值如果小于 0，说明实际拥有的比较多，需要给当前位置以及右侧输出衣服

那么当前位置需要进行的轮数为：

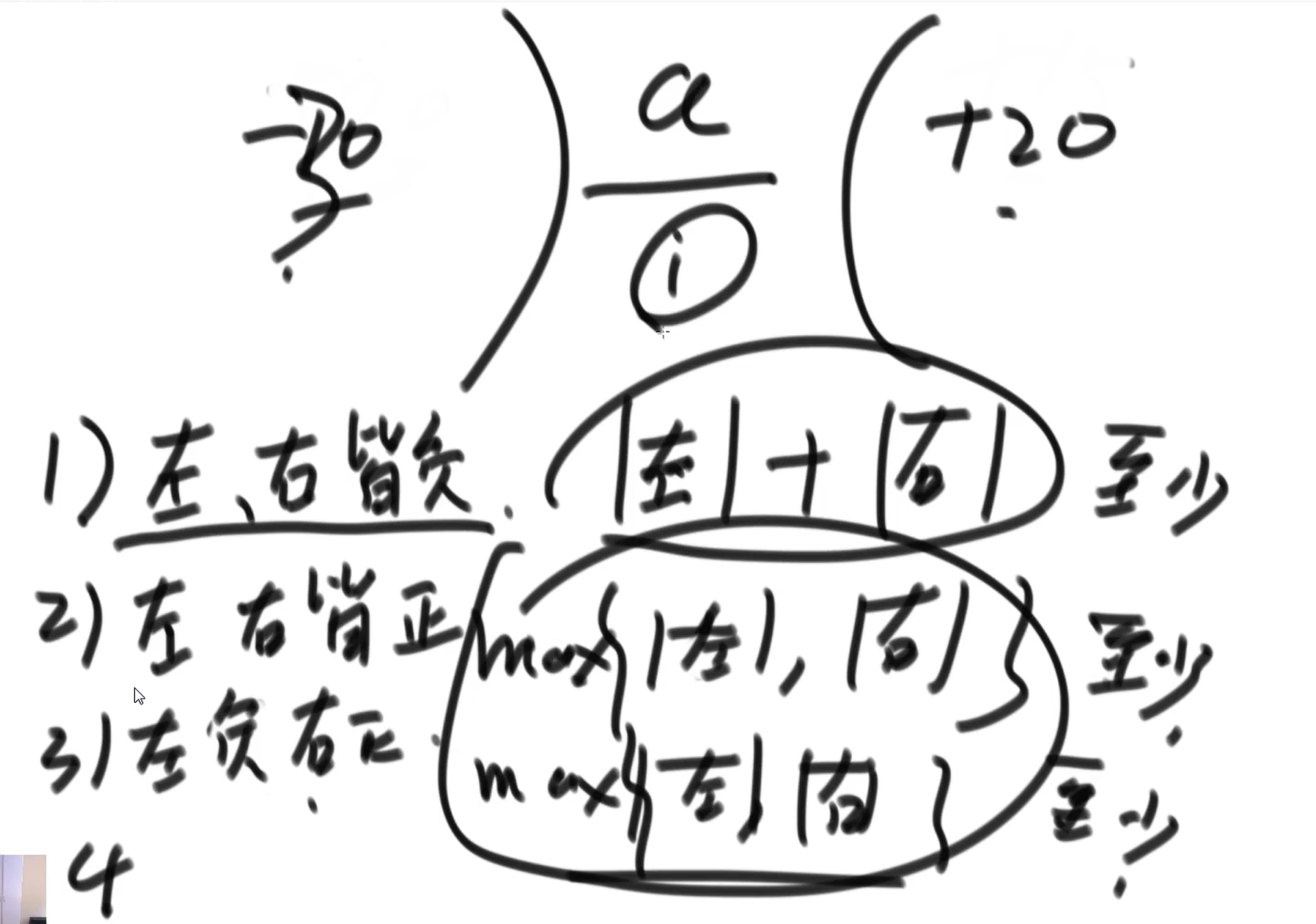
  • 如果 i 位置左右皆为负，代表自己需要给左右提供衣服，那么轮次至少为 |左侧| + |右侧|
  • 如果 i 位置左右一正一负，或者都为正，则轮次至少为 max(|左侧| + |右侧|)

遍历每个位置，计算出最大的值就是系统瓶颈，也就是答案了。

image-20220218165217195

具体的贪心策略：计算出当前位置左侧区域与右侧区域的“衣服总数 - 最终平均分配后剩余的衣服总数”的结果 sub：

  • 如果 sub 为 0，代表这个区域不需要再添加或移走衣服了，已经符合答案要求了
  • 如果当前位置左侧右侧区域的 sub 都为负数，则说明当前位置的衣服太多，两个不够，当前位置的多余的衣服应该分给左右侧区域。执行的操作步数至少为：左右侧的 sub 的绝对值的和，因为每次只能从当前洗衣机移动一件给左或右侧区域
  • 如果当前位置左右侧的 sub 一正一负，则说明一侧多，一侧少，那么执行的步骤至少为：左右侧的 sub 的绝对值的最大值：最大值将其一部分给右侧区域，一部分给当前位置如果当前位置左右侧的sub，瓶颈就在衣服更多的那一侧
  • 如果当前位置左右侧的 sub 都为正，则说明左右侧都多，都应该给当前位置，那么执行的步骤至少为：左右侧的 sub 的绝对值的最大值：左右侧同时给当前位置衣服，那么瓶颈就在衣服更多的那一侧，要等他都给完（少的那一侧是和多的那一侧同时给的，所以已经给完了）

将左侧和右侧区域是为一个整体，加入最左侧缺一个，最右侧多一个，那么只需要一步就可以把最右侧的移动给最左侧（每一台都把一件给左边的，该过程是同步的，是被视为一步的）

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
    public int findMinMoves(int[] machines) {
        if (machines == null || machines.length == 0) {
            return -1;
        }
        int N = machines.length;
        // 先判断所有衣服是否能被整除
        int sum = 0;
        for (int i = 0; i < N; i++) {
            // 计算当前位置左侧（包含当前位置）的总和
            sum += machines[i];
        }
        if ((sum % N) != 0) {
            // 如果不能整除，则肯定不行
            return -1;
        }

        int leftSub = 0;
        int rightSub = 0;
        int leftSum = 0;
        int avg = sum / N;
        int ans = 0;
        // 数组的前缀累加和技巧，遍历过程中更新左侧区域的累加和
        for (int i = 0; i < N; i++) {
            // 计算左侧区域的sub
            leftSub =  leftSum - avg * i;
            // 计算右侧区域的sub
            rightSub = (sum - leftSum - machines[i]) - avg * (N - i - 1);
            if (leftSub < 0 && rightSub < 0) {
                // 1. 都为负，取二者绝对值的和
                ans = Math.max(ans, Math.abs(leftSub) + Math.abs(rightSub));
            } else {
                // 2/3/4. 取绝对值的最大值
                ans = Math.max(ans, Math.max(Math.abs(leftSub), Math.abs(rightSub)));
            }
            // 记得更新leftSum
            leftSum += machines[i];
        }
        return ans;
    }
}

吃苹果最大数目

有一棵特殊的苹果树，一连 n 天，每天都可以长出若干个苹果。在第 i 天，树上会长出 apples[i] 个苹果，这些苹果将会在 days[i] 天后（也就是说，第 i + days[i] 天时）腐烂，变得无法食用。也可能有那么几天，树上不会长出新的苹果，此时用 apples[i] == 0 且 days[i] == 0 表示。

你打算每天 最多 吃一个苹果来保证营养均衡。注意，你可以在这 n 天之后继续吃苹果。给你两个长度为 n 的整数数组 days 和 apples ，返回你可以吃掉的苹果的最大数目。

贪心策略：到了每天，先吃最先过期的苹果，用一个优先级队列维护二元数组（过期的那一天，苹果数量），代表在这一天将有某些数量的苹果过期

  • 阶段一：每到一天，先将堆中的过期的苹果弹出；然后吃掉一个苹果（更新堆顶二元数组的苹果数量，如果吃成0了，也弹出）
  • 阶段二：当过了n 天后，树不会再长苹果了，只能吃。此时每次计算堆苹果数组，取Math.min(过期天数 - 当前天数i, 苹果数量)，重复该过程直到堆空

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
public int eatenApples(int[] apples, int[] days) {
    if (apples == null || days == null || apples.length != days.length) {
        return 0;
    }
    // 贪心算法：到了每天，先吃最先过期的苹果，用一个优先级队列维护二元数组（过期天数，苹果数量）
    // 阶段一：
    //   每到一天，先将堆中的过期的苹果弹出；然后吃掉一个苹果（更新堆顶二元数组的苹果数量，如果吃成0了，也弹出）
    // 阶段二：
    //   当过了n天后，树不会再长苹果了，只能吃。此时每次计算堆苹果数组，取 Math.min(过期天数 - 当前天数i, 苹果数量)，重复该过程直到堆空 
    int n = apples.length;
    // 按照过期天数排序
    PriorityQueue<int[]> heap = new PriorityQueue<>((o1, o2) -> o1[0] - o2[0]);
    int[] cur = null;
    int res = 0;
    int i = 0;
    // 阶段一
    for (; i < n; i++) {
        // 1. 当前天数的苹果先加进去（如果当前天的days==0，不加入）
        if (apples[i] != 0) {
            heap.add(new int[]{i + days[i], apples[i]});
        }

        // 2. 更新当前堆，令过期的弹出
        while (!heap.isEmpty()) {
            cur = heap.peek();
            // 如果当前天就过期了，弹出
            if (cur[0] <= i) {
                heap.poll();
            } else {
                // 如果没过期，则停止while循环
                break;
            }
        }

        // 3. 堆顶苹果数量-1
        if (!heap.isEmpty()) {
            cur = heap.peek();
            // 最先过期的苹果数量减一
            if (--cur[1] == 0) {
                heap.poll();
            }
            res++;
        }
    }

    // 阶段二：
    while (!heap.isEmpty()) {
        // 先加一步是否过期更保险
        if (heap.peek()[0] <= i) {
            heap.poll();
            continue;
        }
        // 能到这里说明当前堆顶在当前天i不过期
        cur = heap.poll();    
        // 那么就取过期时间差与苹果数量的最小值，代表一口气吃这么多（同时跳过这些天数）
        int day = Math.min(cur[0] - i, cur[1]);
        res += day;
        // i直接跳day天
        i += day;
    }

    return res;
}

跳跃游戏 I

55. 跳跃游戏：给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

贪心策略：依次遍历数组中的每一个位置，并实时维护 最远可以到达的位置。对于当前遍历到的位置 x，如果它在 最远可以到达的位置 的范围内，那么我们就可以从起点通过若干次跳跃到达该位置，因此我们可以用 x + nums[x] 更新 最远可以到达的位置。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public boolean canJump(int[] nums) {
    if (nums == null || nums.length == 0) {
        return false;
    }

    int mostRight = 0;
    for (int i = 0; i < nums.length; i++) {
        if (i <= mostRight) {
            // 更新最远距离，看看当前位置作为新的起跳点能否跳的更远 nums[i] + i
            mostRight = Math.max(mostRight, nums[i] + i);
            if (mostRight >= nums.length - 1) {
                return true;
            }
            continue;
        }
        return false;
    }

    return true;
}

跳跃游戏 II

45. 跳跃游戏 II：给你一个非负整数数组 nums，你最初位于数组的第一个位置。数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。假设你总是可以到达数组的最后一个位置。

贪心策略：遍历过程中，在当前区间内 [preEnd, end] 的某个位置起跳，记录其起跳后的最远距离 mostRight。在 i 遍历到当前区间的 end 位置时才开始真正的“逻辑”起跳，因为只有遍历完才知道该在哪里起跳。逻辑起跳后，step++，同时更新下一个区间的 end 为 mostRight。

注意逻辑起跳的概念（提前预约起跳，但还没真正起跳），只是记录了下次起跳后能到达的最远位置，并未真正起跳

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public int jump(int[] nums) {
    if (nums == null || nums.length == 0) {
        return 0;
    }
    // 贪心策略：
    // 遍历过程中，在当前区间内[preEnd, end]的某个位置起跳，记录其起跳后的最远距离mostRight
    // 在 i 遍历到当前区间的 end 位置时才开始真正的“逻辑”起跳，因为只有遍历完才知道该在哪里起跳
    // 逻辑起跳后，step++，同时更新下一个区间的end为mostRight

    int step = 0;
    int mostRight = 0;
    int end = 0;
    // 注意不能带上最后一个位置，因为到了该位置就代表跳完了
    for (int i = 0; i < nums.length - 1; i++) {
        // 在当前区间内遍历寻找下一个起跳点，使得其能跳到最远的位置，更新该位置，作为下一次的end
        mostRight = Math.max(mostRight, nums[i] + i);

        // 到了区间末尾，代表该真正起跳了（前面一直在记录此时真正的起跳点和最远位置）
        if (i == end) {
            // 进入此处代表到了下一次的起跳时机，但是并不一定在当前位置起跳（可不一定在当前区间end位置起跳），
            // 而是在上一个区间的end到当前end之间的这个区间内的某个位置起跳，跳到了最远的mostRight的位置
            step++;
            // 此时的step++代表逻辑上预约了下一次的跳跃，其实际要跳跃到的位置是mostRight，
            // 但是因为程序还没遍历到那么远，此时的跳跃只是逻辑跳跃，当前位置还停留在这个区间内的某个位置上，但是代表提前预约了这个跳跃动作

            // 这一次的起跳，将跳到这个区间内能跳到的最远的位置mostRight处
            // 但是注意此时只是逻辑跳跃，还没真正跳跃，只是先更新了下一次的边界而已
            end = mostRight;
        }
    }

    return step;
}

Magic 操作

给一个包含n个整数元素的集合a，一个包含m个整数元素的集合b。定义magic操作为，从一个集合中取出一个元素，放到另一个集合里，且操作过后每个集合的平均值都大大于于操作前。注意以下两点：

  • 不可以把一个集合的元素取空，这样就没有平均值了
  • 值为x的元素从集合b取出放入集合a，但集合a中已经有值为x的元素，则a的平均值不变（因为集合元素不会重复），b的平均值可能会改变（因为x被取出了）

问最多可以进行多少次magic操作？

规律：

  • 平均值相等时，无论如何都无法做 Magic 操作。因为不论拿出大于平均值、等于平均值还是小于平均值的数字，都会使得两个集合中至少有一个不符合要求
  • 平均值不相等时：
    • 永远不可能从小的集合里拿出放到大的集合里。因为小的集合里拿出大的会让自己均值变小，拿出小的或相等的，会让对方的均值变小
    • 只能从大的集合里拿出放到小的集合里（并且该数字在小集合里不存在）。而且需要拿出大于小的集合均值，且小于大的集合均值的数字

因此，流程为：

  • 先区分两个集合的均值大小。选出大的集合与小的集合的均值间的范围，例如 (50, 100)，只有这些范围的数字可以从大的集合中拿出放到小的集合里。
  • 每次拿出时，贪心策略为：先拿出该区间内的最小的数字（前提是不能在小集合中存在）。

思想：从大集合中先拿出最小的一个值，意味着该数字对大集合是最拖后腿的值，将其去掉后，能最大程度的提高大集合的均值。同时最小的值也意味着，该值是对小集合均值最小幅度的提升。这样就能使得进行 Magic 操作的次数尽量多。

代码实现时，需要在每次移动前，判断该值是否小于当前大集合的平均值（平均值会随着数组的变化而变化，需要在每次移动数字前重新计算）并且大于小集合的平均值。同时还需要判断该值是否已经在小集合中存在（存在的数字不能移动）。并且需要使用 double 类型计算均值，防止整数类型的均值丢失精度从而造成区间计算错误

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
// 请保证arr1无重复值、arr2中无重复值，且arr1和arr2肯定有数字
public static int maxOps(int[] arr1, int[] arr2) {
    double sum1 = 0;
    for (int i = 0; i < arr1.length; i++) {
        sum1 += (double) arr1[i];
    }
    double sum2 = 0;
    for (int i = 0; i < arr2.length; i++) {
        sum2 += (double) arr2[i];
    }
    if (avg(sum1, arr1.length) == avg(sum2, arr2.length)) {
        return 0;
    }
    int[] arrMore = null;
    int[] arrLess = null;
    double sumMore = 0;
    double sumLess = 0;
    if (avg(sum1, arr1.length) > avg(sum2, arr2.length)) {
        arrMore = arr1;
        sumMore = sum1;
        arrLess = arr2;
        sumLess = sum2;
    } else {
        arrMore = arr2;
        sumMore = sum2;
        arrLess = arr1;
        sumLess = sum1;
    }
    Arrays.sort(arrMore);
    HashSet<Integer> setLess = new HashSet<>();
    for (int num : arrLess) {
        setLess.add(num);
    }
    int moreSize = arrMore.length;
    int lessSize = arrLess.length;
    int ops = 0;
    for (int i = 0; i < arrMore.length; i++) {
        double cur = (double) arrMore[i];
        if (cur < avg(sumMore, moreSize) && cur > avg(sumLess, lessSize)
            && !setLess.contains(arrMore[i])) {
            sumMore -= cur;
            moreSize--;
            sumLess += cur;
            lessSize++;
            setLess.add(arrMore[i]);
            ops++;
        }
    }
    return ops;
}

组成三角形

在迷迷糊糊的大草原上，小红捡到了n根木棍，第i根木棍的长度为i，小红现在很开心。想选出其中的三根木棍组成美丽的三角形。但是小明想捉弄小红，想去掉一些木棍，使得小红任意选三根木棍都不能组成三角形。

请问小明最少去掉多少根木棍呢？给定N，返回至少去掉多少根？

思路：该题的贪心策略是：在N个木棍中，保留符合斐波那契数列的木棍，其余都去掉，就能保证是去掉最少的木棍。

例如，给定N=17，则就从 [1, 17] 中选出斐波那契数列：1, 2, 3, 5, 8, 13。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static int minDelete(int m) {
    if (m < 4) {
        return 0;
    }
    int k_2 = 2;
    int k_1 = 3;
    int num = 3;
    while (k_2 + k_1 <= m) {
        num++;
        // k_1 更新到新的斐波那契值
        k_1 += k_2;
        // k_2 等于刚才的 k_1
        k_2 = k_1 - k_2;
    }
    // 返回需要去除几根
    return m - num;
}

预处理技巧

染色问题

牛牛有一些排成一行的正方形。每个正方形已经被染成红色或者绿色。牛牛现在可以选择任意一个正方形然后用这两种颜色的任意一种进行染色,这个正方形的颜色将会被覆盖。牛牛的目标是在完成染色之后,每个红色R都比每个绿色G距离最左侧近。牛牛想知道他最少需要涂染几个正方形。如样例所示：s = RGRGR

我们涂染之后变成 RRRGG 满足要求了，涂染的个数为2，没有比这个更好的涂染方案。

思路：遍历每一个位置，以当前位置为分界线，

  • 统计左侧有多少个G，将其染成R
  • 统计右侧有多少个R，将其染成G
  • 二者的和就是当前位置作为分界线时的涂染个数。

但如果每到一个位置都需要遍历左右侧的区间统计R和G的个数，则时间复杂度为 O(N^2)。我们可以使用预处理技巧：先遍历两遍数组，分别统计出每个位置左侧有多少个G，以及每个位置右侧有多少个R，然后再遍历一遍数组，就可以使用预处理的数组快速计算出当前位置的染色数量，从而加速算法。进一步优化：预处理时只遍历right数组，然后在遍历left数组的过程中就可以计算答案。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
public class ColorLeftRight {
    public static int minPaint(String s) {
        if (s == null || s.length() < 1) {
            return 0;
        }
        char[] str = s.toCharArray();
        int N = str.length;
        /*
		 * 遍历每一个位置, 以当前位置为分界线:
		 * 1. 统计左侧有多少个G, 将其染成R.
		 * 2. 统计右侧有多少个R, 将其染成G.
		 * 遍历每个位置后, 即可得到染色最少的方案
		 * 这种方法的时间复杂度为 O(N^2)
		 */
        // for (int i = 0; i <= N; i++) {
        // 	if (i == 0) {
        // 		// 如果分界线在0位置, 代表左侧不需要染色, 需要统计右侧有多少个R
        // 	} else if (i == N) {
        // 		// 如果分界线在N位置, 代表右侧不需要染色, 需要统计左侧有多少个G
        // 	} else {
        // 		// 否则将数组划分为 [0, i - 1] 与 [i, N - 1]
        // 		// 分别统计左侧有多少个G与右侧有多少个R
        // 	}
        // }

        /*
		 * 预处理技巧: 先遍历两遍数组, 分别统计出每个位置左侧有多少个G, 以及每个位置右侧有多少个R,
		 * 然后再遍历一遍数组, 就可以使用预处理的数组快速计算出当前位置的染色数量, 从而加速算法
		 * 进一步优化: 预处理时只遍历right数组, 然后在遍历left数组的过程中就可以计算答案
		 */
        int[] right = new int[N];
        // 初始化最后一个位置的值
        right[N - 1] = str[N - 1] == 'R' ? 1 : 0;
        // 倒序遍历数组, 更新right数组
        for (int i = N - 2; i >= 0; i--) {
            right[i] = right[i + 1] + (str[i] == 'R' ? 1 : 0);
        }

        // 正向遍历数组, 使用变量left记录目前位置左侧G的数量, 就可以省掉一次left数组的创建
        int left = 0;
        int res = Integer.MAX_VALUE;
        //
        for (int i = 0; i <= N; i++) {
            if (i == 0) {
                // 如果分界线在0位置, 代表左侧不需要染色, 需要统计右侧有多少个R
                res = right[0];
            } else if (i == N) {
                // 如果分界线在N位置, 代表右侧不需要染色, 需要统计左侧有多少个G
                left += str[i - 1] == 'G' ? 1 : 0;
                res = Math.min(res, left);
            } else {
                // 否则将数组划分为 [0, i - 1] 与 [i, N - 1]
                // 分别统计左侧[0, i-1]有多少个G, 以及右侧right[i]有多少个R
                // [0, i - 1]: 'G'的数量 = left + str[i-1]是否是'G'
                left += str[i - 1] == 'G' ? 1 : 0;
                res = Math.min(res, right[i] + left);
            }
        }
        return res;
    }

    public static void main(String[] args) {
        System.out.println(minPaint("GGGGGR"));
    }
}

最大的正方形边框

image-20211220150352356

最暴力的方法：遍历矩阵中的每一个位置，在该位置处遍历此处可以支持的边框的大小（扩到矩阵边界为止），然后遍历该边框内的值，判断是否都是1。这种方式时间复杂度为 O(N^4)，不可采纳。

预处理技巧：

1、判断边框内是否都为1：创建两个辅助数组 right 和 down，分别保存：

  • right[]：包含当前位置在内，往后连续为1的个数，多扩一列（为了最后一列的计算方便）
  • down[]：包含当前位置在内，往下连续为1的个数，多扩一行（为了最后一行的计算方便）

注意：这里的 right 和 down 的范围要比原矩阵多一列和一行，这样就能快速计算出最后一行和最后一列的值，不需要单独初始化最后一行和最后一列。

事先遍历一遍整个矩阵，将 right 和 down 内的值初始化完毕，后面使用该矩阵即可快速计算出当前框内是否都为1。方法为：判断边框左上角，右上角和左下角的 right/down 中的值即可：

1
2
3
4
5
6
// 判断当前框内是否都是1
if (right[i][j] >= size && down[i][j] >= size
    && right[i + size - 1][j] >= size
    && down[i][j + size - 1] >= size) {
    return true;
}

2、遍历矩阵：不同于正向思维中遍历到每一个位置后再遍历可能的边框情况。我们选用逆向思维，先确定边框的范围（从大到小），然后再判断在当前边框大小的情况下，原矩阵中哪些位置可以作为边框的左上角被遍历到，在这些左上角位置开始调用封装好的方法判断此位置画框能否都是1。这样就能从边框最大的情况开始，一旦找到了该边框尺寸情况下某个位置都是1，则就可以直接返回了，不需要再遍历更小边框的情况了，无疑节省了大量时间。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
public class MaxBorderSize {
    public static int getMaxBorderSize(int[][] m) {
        if (m == null || m.length < 1) {
            return 0;
        }
        // right: 包含当前位置在内, 往后连续为1的个数，多扩一列（为了最后一列的计算方便）
        // down: 包含当前位置在内, 往下连续为1的个数，多扩一行（为了最后一行的计算方便）
        int[][] right = new int[m.length][m[0].length + 1];
        int[][] down = new int[m.length + 1][m[0].length];

        // 设置right和down的值
        setBorderMapSimple(m, right, down);
        // size从最大开始取, 遍历每一个可行的位置, 判断当前大小的边界是否都是1
        for (int size = Math.min(m.length, m[0].length); size > 0; size--) {
            if (meets(m, right, down, size)) {
                return size;
            }
        }
        return 0;
    }

    private static boolean meets(int[][] m, int[][] right, int[][] down, int size) {
        int row = m.length;
        int col = m[0].length;
        // 遍历此时可以画框的位置, 判断该正方形的三个点: m[i][j] m[i+size-1][j] m[i][j+size-1] 在right和down中的值
        for (int i = 0; i < row - size + 1; i++) {
            for (int j = 0; j < col - size + 1; j++) {
                // 判断当前框内是否都是1
                if (right[i][j] >= size && down[i][j] >= size
                    && right[i + size - 1][j] >= size
                    && down[i][j + size - 1] >= size) {
                    return true;
                }
            }
        }
        return false;
    }

    // 不推荐
    public static void setBorderMap(int[][] m, int[][] right, int[][] down) {
        int row = m.length;
        int col = m[0].length;
        // 先初始化最后一行最后一列
        if (m[row - 1][col - 1] == 1) {
            right[row - 1][col - 1] = 1;
            down[row - 1][col - 1] = 1;
        }

        // 初始化最后一列
        for (int i = row - 2; i >= 0; i--) {
            // 当前位置如果为1, 则更新其下面连续的1的个数
            if (m[i][col - 1] == 1) {
                // 更新每一行最后一列的right矩阵
                right[i][col - 1] = 1;
                // 更新down矩阵为下一行的值加一
                down[i][col - 1] = down[i + 1][col - 1] + 1;
            }
        }
        // 初始化最后一行
        for (int j = col - 2; j >= 0; j--) {
            // 当前位置如果为1, 则更新其下面连续的1的个数
            if (m[row - 1][j] == 1) {
                // 更新每一列最后一行的down矩阵
                down[row - 1][j] = 1;
                // 更新down矩阵为下一行的值加一
                right[row - 1][j] = right[row - 1][j + 1] + 1;
            }
        }
        // 更新其他行与列(从倒数第二行倒数第二列开始)
        for (int i = row - 2; i >= 0; i--) {
            for (int j = col - 2; j >= 0; j--) {
                if (m[i][j] == 1) {
                    right[i][j] = right[i][j + 1] + 1;
                    down[i][j] = down[i + 1][j] + 1;
                }
            }
        }
    }

    public static void setBorderMapSimple(int[][] m, int[][] right, int[][] down) {
        int row = m.length;
        int col = m[0].length;
        // 先初始化m矩阵最后一行最后一列的位置
        if (m[row - 1][col - 1] == 1) {
            right[row - 1][col - 1] = 1;
            down[row - 1][col - 1] = 1;
        }

        // 不需要额外初始化最后一行和最后一列了，因为right扩了一列，down扩了一行，恰好能处理最后一行和最后一列
        for (int i = row - 1; i >= 0; i--) {
            for (int j = col - 1; j >= 0; j--) {
                if (m[i][j] == 1) {
                    // right矩阵恰好扩了一列，使得原矩阵最后一列可以取到col-1 + 1的位置（0）
                    right[i][j] = right[i][j + 1] + 1;
                    down[i][j] = down[i + 1][j] + 1;
                }
            }
        }
    }

    public static int[][] generateRandom01Matrix(int rowSize, int colSize) {
        int[][] res = new int[rowSize][colSize];
        for (int i = 0; i != rowSize; i++) {
            for (int j = 0; j != colSize; j++) {
                res[i][j] = (int) (Math.random() * 2);
            }
        }
        return res;
    }

    public static void printMatrix(int[][] matrix) {
        for (int i = 0; i != matrix.length; i++) {
            for (int j = 0; j != matrix[0].length; j++) {
                System.out.print(matrix[i][j] + " ");
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        int[][] matrix = generateRandom01Matrix(7, 8);
        printMatrix(matrix);
        System.out.println(getMaxBorderSize(matrix));
    }
}