【数据结构】数组与字符串

发表于2021-12-01更新于2022-03-01字数统计3.5k阅读时长27分阅读次数

二维数组常见题目

顺时针打印矩阵

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。

image-20211220183010271

示例 1：

1
2
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

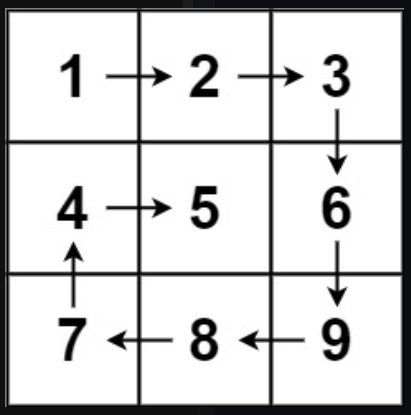
思路：定义两个点：左上角和右下角。这两个点每次都在同一层的边框上，只要确定了这两个点，就可以顺时针方向遍历这一层框的元素（四条边上的元素）。遍历完毕后再将左上角向右下方向移动一格，右下角向左上方向移动一格。从而使得边框向内层收缩，然后重复上一步骤即可。

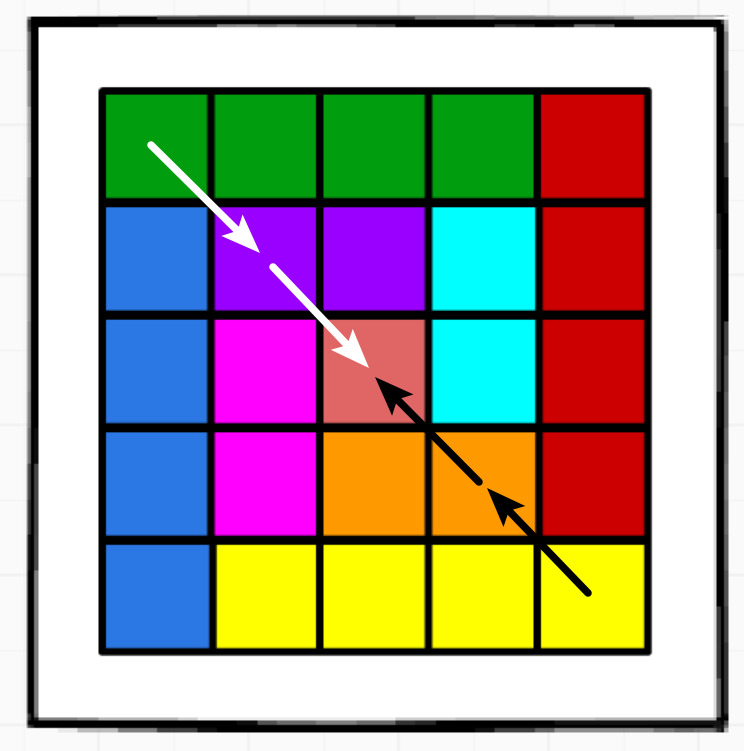
例如下图使用不同颜色代表每一层的各个边，两个箭头代表两个边界点的移动方向：

image-20211220165107072

其中，在打印当前层的边框时，需要特别注意：分别打印四条边时，每次循环的终止是在该边的另一端点（另一条边的起点）的前一个位置，不能将该端点也打印，而应该将其作为下一条边的起点时被打印。以上图为例，最外层的遍历每次只能遍历四个格子，不能遍历到该行/列的最后一个，因为这一个元素是下一条边的起点，不能提前遍历了。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
public class PrintMatrixSpiralOrder {
    public static void printMatrixSpiralOrder(int[][] matrix) {
        if (matrix == null || matrix.length < 1) {
            return;
        }
        int topRow = 0;
        int topCol = 0;
        int downRow = matrix.length - 1;
        int downCol = matrix[0].length - 1;
        while (topRow <= downRow && topCol <= downCol) {
            // 打印当前边界后，左上角向右下移动一步，右下角向左上移动一步，缩小边界框，继续循环
            printEdge(matrix, topRow++, topCol++, downRow--, downCol--);
        }

    }

    public static void printEdge(int[][] matrix, int topRow, int topCol, int downRow, int downCol) {
        if (topRow > downRow || topCol > downCol) {
            // 如果左上角在右下角的右下方，代表越界了，直接返回
            return;
        }
        if (topRow == downRow) {
            // 如果左上角和右下角在同一行，则只需要打印这一行即可
            while (topCol <= downCol) {
                System.out.print(matrix[topRow][topCol] + ' ');
                topCol++;
            }
        } else if (topCol == downCol) {
            // 如果左上角和右下角在同一列，则只需要打印这一列即可
            while (topRow <= downRow) {
                System.out.print(matrix[topRow][topCol] + ' ');
                topRow++;
            }
        } else {
            // 普通情况，四轮循环打印四条边
            int curRow = topRow;
            int curCol = topCol;
            // 注意！！！ curCol 不能等于 downCol，否则在到达角点时，进行curCol++后会使得curCol越界
            while (curCol < downCol) {
                System.out.print(matrix[curRow][curCol] + " ");
                curCol++;
            }
            while (curRow < downRow) {
                System.out.print(matrix[curRow][curCol] + " ");
                curRow++;
            }
            while (curCol > topCol) {
                System.out.print(matrix[curRow][curCol] + " ");
                curCol--;
            }
            while (curRow > topRow) {
                System.out.print(matrix[curRow][curCol] + " ");
                curRow--;
            }
        }
    }

    public static void main(String[] args) {
        int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 },
                          { 13, 14, 15, 16 } };
        printMatrixSpiralOrder(matrix);
    }
}

顺时针旋转正方形

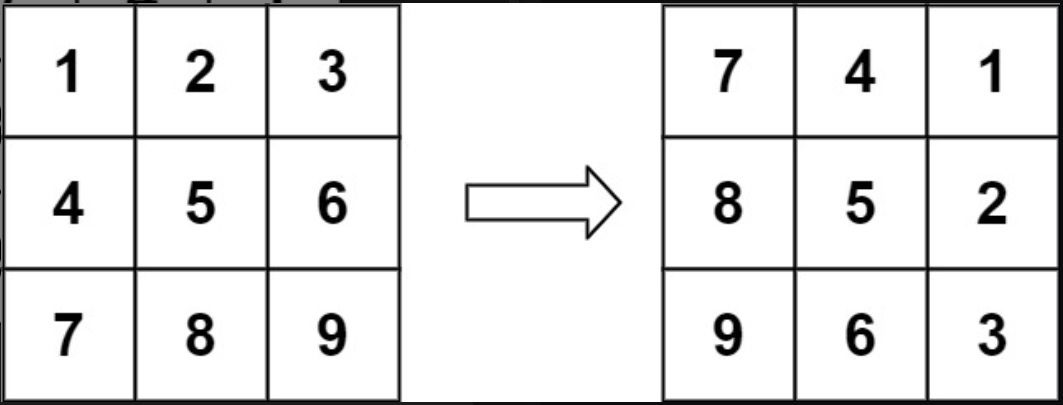
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

image-20211220183127440

方法一：由外向内层层遍历，交换每层内的四个对应位置

同样可以使用上面题目的套路解该题，由外向内一层一层遍历该矩阵，每次将当前层的四条边上的对应位置进行交换。例如，交换如下四个元素：

image-20211220165545301

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
public class RotateMatrix {
    public static void rotateMatrix(int[][] matrix) {
        if (matrix == null || matrix.length == 0) {
            return;
        }
        int topRow = 0;
        int topCol = 0;
        int downRow = matrix.length - 1;
        int downCol = matrix[0].length - 1;
        while (topRow < downRow && topCol < downCol) {
            rotateEdge(matrix, topRow++, topCol++, downRow--, downCol--);
        }
    }

    public static void rotateEdge(int[][] matrix, int topRow, int topCol, int downRow, int downCol) {
        if (topRow > downRow || topCol > downCol) {
            return;
        }
        int tmp = 0;
        // 当前框内每一组有total个元素
        int total = downCol - topCol;
        // 正方形矩阵，不会发生左上角与右下角共行/列的情况
        // 遍历四组中的每一个元素i，将其与其他组的位置交换
        // 注意不能包含 downCol 列，因为该位置是属于第二组的第一个元素，不属于第一组
        for (int i = 0; i < total; i++) {
            tmp = matrix[topRow][topCol + i];
            // 第一组的值改为第四组的对应位置
            matrix[topRow][topCol + i] = matrix[downRow - i][topCol];
            // 第四组的值改为第三组的对应位置
            matrix[downRow - i][topCol] = matrix[downRow][downCol - i];
            // 第三组的值改为第二组的对应位置
            matrix[downRow][downCol - i] = matrix[topRow + i][downCol];
            // 第二组的值改为第一组的对应位置
            matrix[topRow + i][downCol] = tmp;
        }
    }

    public static void printMatrix(int[][] matrix) {
        for (int i = 0; i != matrix.length; i++) {
            for (int j = 0; j != matrix[0].length; j++) {
                System.out.print(matrix[i][j] + " ");
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 },
                          { 13, 14, 15, 16 } };
        printMatrix(matrix);
        rotateMatrix02(matrix);
        System.out.println("=========");
        printMatrix(matrix);
    }
}

方法二：上下翻转 + 对角翻转

使用数学规律，先将数组上下翻转，然后沿着对角线反转，同样可以得到答案。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 方法二：使用数学规律，先将数组上下翻转，然后沿着对角线反转
public static void rotateMatrix02(int[][] matrix) {
    if (matrix == null || matrix.length == 0) {
        return;
    }
    int N = matrix.length;
    int tmp = 0;
    // 先上下反转
    for (int i = 0; i < N / 2; i++) {
        for (int j = 0; j < N; j++) {
            // 交换上下对称位置的值
            tmp = matrix[i][j];
            matrix[i][j] = matrix[N - 1 - i][j];
            matrix[N - 1 - i][j] = tmp;
        }
    }
    // 然后沿着对角线反转
    for (int i = 0; i < N; i++) {
        // 注意对角线上的元素不反转
        for (int j = i + 1; j < N; j++) {
            tmp = matrix[i][j];
            matrix[i][j] = matrix[j][i];
            matrix[j][i] = tmp;
        }
    }
}

zigzag 方式打印矩阵

用 zigzag 的方式打印矩阵，比如如下的矩阵

示例：

1
2
3
4
5
矩阵：
  0 1 2 3
  4 5 6 7
  8 9 10 11
打印顺序为：0 1 4 8 5 2 3 6 9 10 7 11

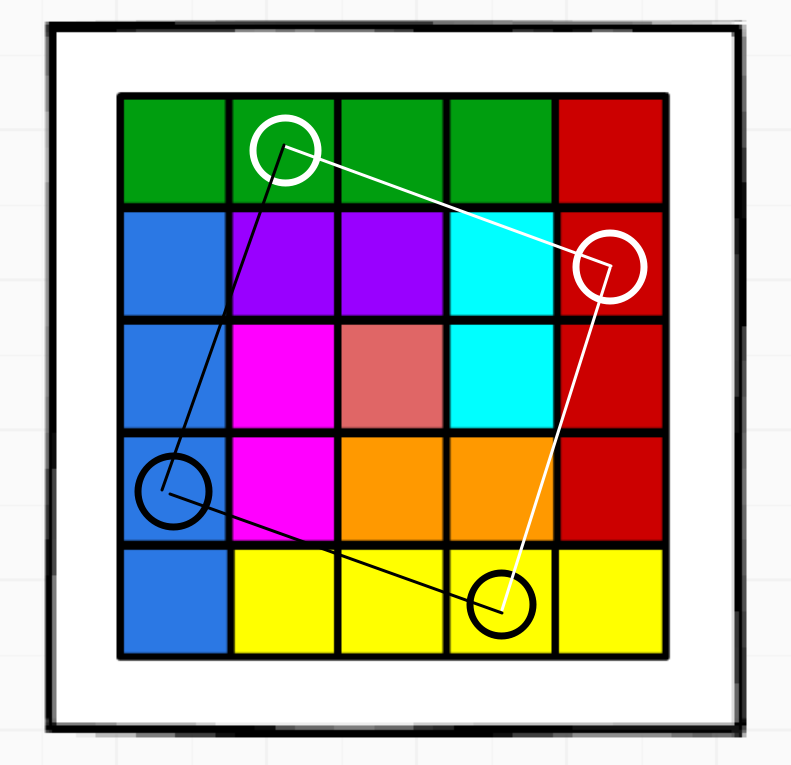
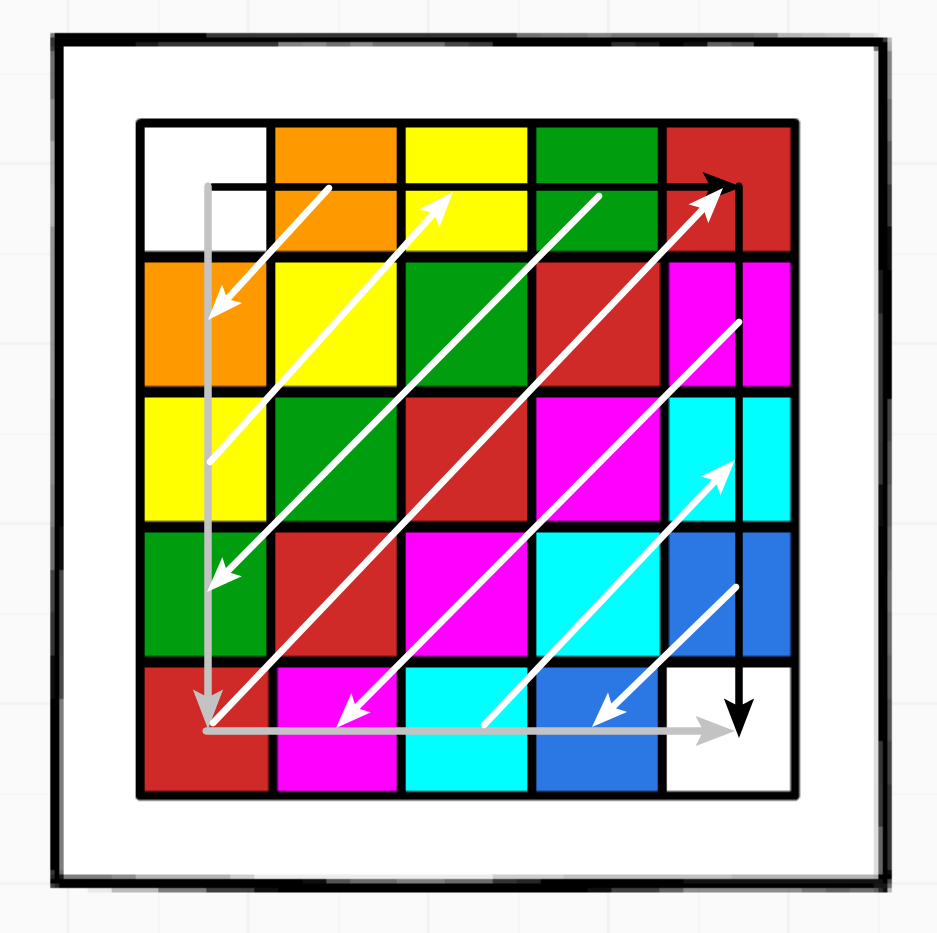
思路：定义两个边界点，分别沿着下图黑色路径与灰色路径移动，二者每次都一起移动一格。如果遇到边界就拐弯。二者每一起运动一格后，就打印二者构成的对角线上的元素（交替顺序，一次向上，一次向下），最终二者相遇在右下角时全部打印完毕。

image-20211220170626523

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
public class ZigZagPrintMatrix {
    public static void zigZagPrint(int[][] matrix) {
        if (matrix == null || matrix.length == 0) {
            return;
        }
        // 上边界
        int topRow = 0;
        int topCol = 0;
        // 下边界
        int downRow = 0;
        int downCol = 0;
        // 右下角点（终止点）
        int endRow = matrix.length - 1;
        int endCol = matrix[0].length - 1;

        boolean fromUp = false;
        // 将在右下角相遇，然后退出循环
        while (topRow <= endRow) {
            printLine(matrix, fromUp, topRow, topCol, downRow, downCol);
            // 上边界点一直右移，直到移动到最后一列后开始向下移动

            // 注意 ⬇⬇⬇ 两个边界点移动时的顺序非常重要，因为行会受到列的影响或列会受到行的影响

            // 注意！！上边界要先更新行，因为行会受到列的影响，而列不会受到行的影响。要先更新会受影响的变量
            // 如果先更新列，那么可能在边角处漏掉一个位置元素
            topRow = topCol == endCol ? topRow + 1: topRow;
            topCol = topCol == endCol ? topCol : topCol + 1;
            // 下边界点一直下移，直到移动到最后一行后开始向右移动
            // 注意！！下边界要先更新列，因为列会受到行的影响，而行不会受到列的影响。要先更新会受影响的变量
            // 如果先更新行，那么可能在边角处漏掉一个位置元素
            downCol = downRow == endRow ? downCol + 1: downCol;
            downRow = downRow == endRow ? downRow : downRow + 1;

            // 交替上下打印，每次取反
            fromUp = !fromUp;
        }
    }

    public static void printLine(int[][] matrix, boolean fromUp, int topRow, int topCol, int downRow, int downCol) {
        if (fromUp) {
            // 从上到下打印
            while (topRow <= downRow) {
                System.out.print(matrix[topRow++][topCol--] + " ");
            }
        } else {
            // 从下到上打印
            while (topRow <= downRow) {
                System.out.print(matrix[downRow--][downCol++] + " ");
            }
        }
    }

    public static void main(String[] args) {
        int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 } };
        zigZagPrint(matrix);
    }
}

KMP 算法

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
public class KMP {

    // 整体时间复杂度：O(N)，N 为 s 的长度
    public static int getIndexOf(String s, String m) {
        if (s == null || m == null || m.length() < 1 ||  s.length() < m.length()) {
            return -1;
        }

        char[] str1 = s.toCharArray();
        char[] str2 = m.toCharArray();
        int[] next = getNextArray(str2);
        int i1 = 0;
        int i2 = 0;

        while (i1 < str1.length && i2 < str2.length) {
            if (str1[i1] == str2[i2]) {
                // 情况一：当前位置相同，则一起往后移动
                i1++;
                i2++;
            } else if (next[i2] == -1) {
                // 情况二：str2 都到0位置了，还是和 str1 匹配不了。那么此时 str1 需要换一个开头和 str2 比较
                // 等价于 i2 == 0，说明 i2 回到了原点，没有前缀了，也就没有办法再继续用技巧往右跳了
                i1++;
            } else {
                // 情况三：当前的 X 和 Y 不相同，但是 Y 又不是 0，说明此时 str2 中 0 ~ Y-1 上的字符串和 str1 中已经有重合了，
                // 但是 Y 位置却和 X 不同，说明 Y 该调出其最大前缀，使用技巧直接跳过这些字符到 next[i2] 位置
                // PS：[0, i2 -1] 范围内的字符串肯定和 [Y-1 - (i2-1) , Y-1] 上的字符串完全匹配，所以可以直接跳到 i2 位置继续匹配
                // str1 的 X 位置固定不动，str2 的 Y 使用技巧跳过重复的前缀元素
                i2 = next[i2];
            }
        }
        return i2 == str2.length ? i1 - i2 : -1;
    }

    // 时间复杂度：O(M)，M 为 str 的长度
    public static int[] getNextArray(char[] str) {
        if (str.length == 1) {
            return new int[]{ -1 };
        }

        int[] next = new int[str.length];
        // 前两个位置的值是固定的
        next[0] = -1;
        next[1] = 0;

        // i 代表遍历 str 过程中当前的位置
        int i = 2;
        // cn 代表在遍历过程中，每个 i-1 位置对应的最大前缀值：next[i-1]。当前 i 位置需要使用该值进行计算得到 next[i] 的值
        // cn：当前位置 i 的前一个位置 i-1 的最大前缀子串的下一个字符在什么位置，即 cn == next[i-1]
        // 该位置的字符需要和 i-1 位置的字符比较是否相同，相同则 i 位置的最大前缀为 next[i-1] + 1，否则继续向前跳计算新的 cn
        int cn = 0;

        while (i < str.length) {
            if (str[cn] == str[i - 1]) {
                // 情况一：cn 位置的值等于 i-1 位置的值，则当前 i 位置的最大前缀子串长度为 next[i-1] + 1
                // i++：将进行下一个位置的计算；++cn：下一个位置的cn要更新了，因为i位置的最大前缀加了1，所以下一个位置也要+1
                next[i++] = ++cn;
            } else if (cn > 0) {
                // 注意：判别条件是 cn > 0，不是 next[cn] > 0
                // 情况二：当前跳到 cn 位置的字符，和 i-1 位置字符匹配不上时，cn 继续向前跳
                // 注意：cn 更新为当前 cn 的最大前缀子串的下一个字符位置，即 next[cn]
                cn = next[cn];
            } else {
                // 情况三：如果无法往前跳了，则当前位置i不存在重合区间
                // 注意：i 要 ++，进行更新
                next[i++] = 0;
            }
        }
        return next;
    }
}

Man

字符串常见题目

翻转单词顺序

输入一个英文句子，翻转句子中单词的顺序，但单词内字符的顺序不变。为简单起见，标点符号和普通字母一样处理。例如输入字符串"I am a student. “，则输出"student. a am I”。 说明：

  • 无空格字符构成一个单词。
  • 输入字符串可以在前面或者后面包含多余的空格，但是反转后的字符不能包括。
  • 如果两个单词间有多余的空格，将反转后单词间的空格减少到只含一个。

示例 1：

1
2
输入: "the sky is blue"
输出: "blue is sky the"

示例 2：

1
2
3
输入: "  hello world!  "
输出: "world! hello"
解释: 输入字符串可以在前面或者后面包含多余的空格，但是反转后的字符不能包括。

示例 3：

1
2
3
输入: "a good   example"
输出: "example good a"
解释: 如果两个单词间有多余的空格，将反转后单词间的空格减少到只含一个。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
// 我自己的：
public String reverseWords(String s) {
    if (s == null || s.length() < 1) {
        return s;
    }

    List<String> list = new ArrayList<>();
    int left = 0;
    int right = 0;
    int count = 0;
    // 1. 遍历过程中将首尾空格去掉，然后使用left和right将中间的多个空格去掉
    for (; right < s.length(); right++) {
        if (s.charAt(right) == ' ') {
            if (left != right) {
                list.add(s.substring(left, right));
                count++;
                left = right + 1;
            } else {
                left++;
            }
        }
    }
    // right遍历完后记得再额外判断一次最后的[left, right]区间
    if (left != right) {
        list.add(s.substring(left, right));
        count++;
    }


    StringBuilder sb = new StringBuilder();

    // 2. 倒序遍历list，这样就实现了整体的反转
    while (count-- > 0) {
        String substr = list.get(count);
        sb.append(substr);
        if (count != 0) {
            sb.append(' ');
        }
    }
    return sb.toString();
}

// 题解：只需一次遍历
public String reverseWords(String s) {
    // 删除首尾空格
    s = s.trim(); 
    // 也是使用的双指针锁定子字符串区间
    int j = s.length() - 1, i = j;
    StringBuilder res = new StringBuilder();
    // 从后往前倒序遍历
    while(i >= 0) {
        // 搜索首个空格
        while(i >= 0 && s.charAt(i) != ' ') {
            i--; 
        }
        // 添加单词
        res.append(s.substring(i + 1, j + 1) + " "); 
        // 跳过单词间空格
        while(i >= 0 && s.charAt(i) == ' ') {
            i--; 
        }
        // j 指向下个单词的尾字符（更新右指针）
        j = i;
    }
    return res.toString().trim(); // 转化为字符串并返回
}