【数据结构】堆

堆结构

堆结构本身比堆排序要重要

堆结构就是用数组实现的完全二叉树结构。

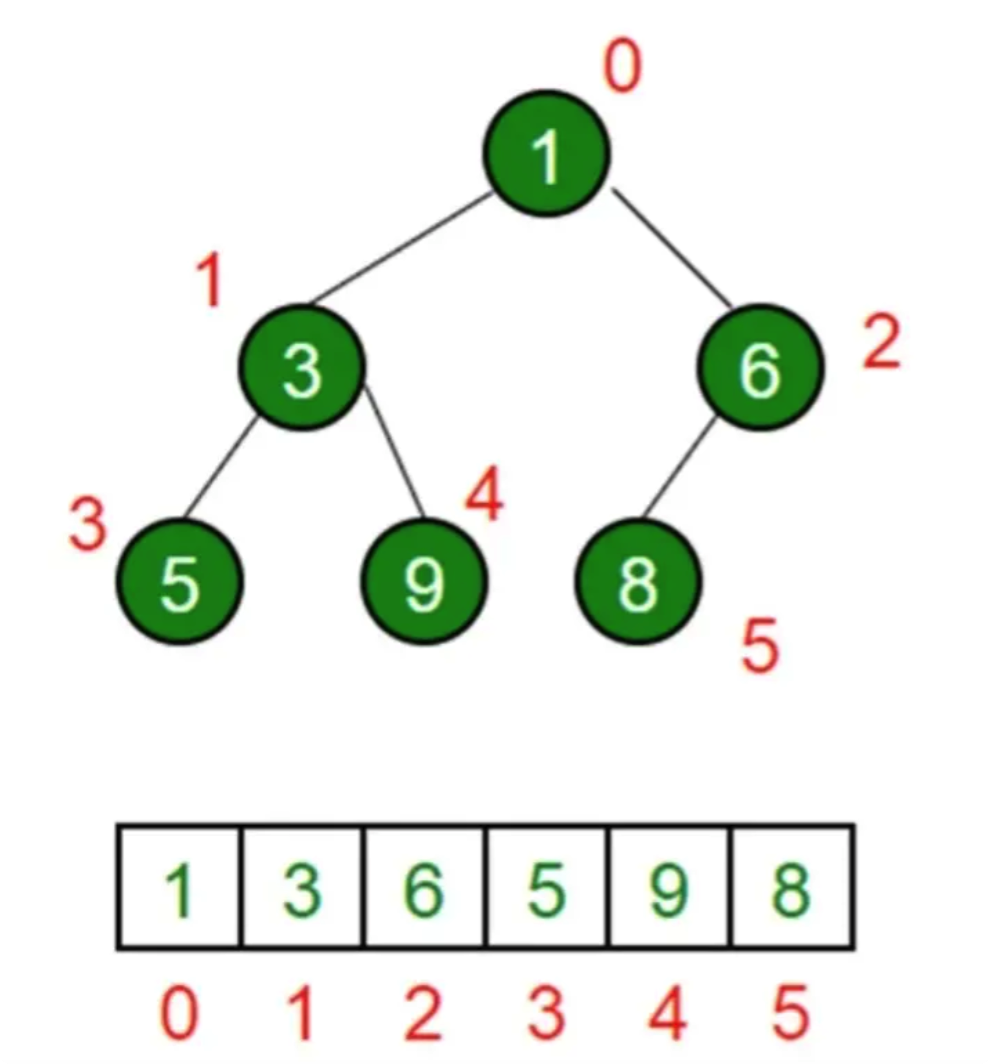
堆结构的节点公式：

节点 i 的父节点为 (i - 1) / 2（左右节点都可以统一用这个公式）
节点 i 的左子节点为 2 * i + 1
节点 i 的右子节点为 2 * i + 2

使用上述公式即直接定位到某个节点的父/子节点

大/小根堆

大根堆：堆中的每一个父节点都要比其子节点上的数字大（不考虑其对称的另一侧分支里的节点数字大小）。
小根堆：堆中的每一个父节点都要比其子节点上的数字小（不考虑其对称的另一侧分支里的节点数字大小）。

堆结构最重要的两个操作：

heapInsert：add 操作，新增一个数据到已知堆中。具体做法是新增的数据不断向上遍历堆结构，将数字插入到合适的父节点位置
heapify：poll 操作，弹出堆里第一个元素（根节点）的值，并重新调整堆结构，令其余部分的元素继续保持大/小根堆结构。具体做法是新的根结点的元素不断向下遍历堆结构，交换其到合适的子节点位置

heapInsert：add 操作。用于新增一个数据到堆中，当新来一个数字时，将其添加到堆结构中，并且满足大根堆（或小根堆）：向上遍历他的每一个父节点，判断其是否大于它的父节点，若大于则和父节点交换，若小于则停止遍历。直到当前数字放到合适的父节点位置，使得当前堆满足大根。

heapify：poll 操作。用于弹出堆中第一个元素，并令其余部分继续保持大/小根堆结构，若用户要求返回并删除当前大根堆的最大元素，并且要求删除后的其他元素依旧符合大根堆：返回当前堆的第一个节点（其肯定是最大元素），然后将当前堆的最后一个元素放到第一个元素的位置。之后开始向下遍历第一个元素的子节点，选出其子节点中最大的数字，并且判断该数字和自身的大小，若子节点数字更大，则交换自身和子节点，若子节点数字更小，则停止遍历；直到该元素被放到合适的子节点位置。

这两个操作的空间复杂度都是 O(logN)，因为 N 个节点的完全二叉树的高度为 O(logN)，上述两个操作都只需要遍历二叉树中的某一条分支即可，因此时间只有 O(logN)

heapInsert 的代码：

public static void heapInsert(int[] arr, int index) {
  // 向上遍历当前节点的父节点,直到满足条件: 父节点的值 > 当前节点的值
  while (arr[(index - 1) / 2] < arr[index]) {
    swap(arr, (index - 1) / 2, index);
    index = (index - 1) / 2; // index 记得变为父节点的值
  }
}

heapify 的代码：

// heapSize 用于表示逻辑上的堆的大小, 其和数组的大小没关系
// 该方法的作用是, 在给定堆结构中, 当某个位置的元素被弹出,替换成了其他数字后
// 要保证新的数组仍然保持堆结构, 那么就需要从这个位置开始向下遍历
// 交换其子节点中最大的元素
public static void heapify(int[] arr, int index, int heapSize){
  if (heapSize > arr.length) {
    return;
  }

  while (2*index+1 < heapSize) {
    // 两个孩子中, 判断谁的值更大
    int largest = (2*index+2 < heapSize) && arr[2*index+1] < arr[2*index+2]
      ? 2*index+2 : 2*index+1;

    // 当前节点和子孩子中, 判断谁的值更大
    largest = arr[index] < arr[largest] ? largest : index;

    // 如果相等, 说明此时已经满足了大根堆的条件, 可以跳出循环
    if (largest == index) {
      break;
    }

    // 交换
    swap(arr, index, largest);
    index = largest;
  }
}

具体应用

若用户要求修改堆结构中任意一个位置的元素的值，并要求修改后的数字仍然满足大根堆，则只需要判断修改后的元素是比原先大还是小：

若修改后的元素比原先大，则进行 heapInsert 操作，将当前元素向上交换到合适的父节点位置
若修改后的元素比原先小，则进行 heapify 操作，将当前元素向下交换到合适的子节点位置

小根堆在 Java 中就是优先级队列默认的实现方式： PriorityQueue<Interger>，其两个方法：

add() ：本质上就是 heapInsert 操作，将一个数字添加到已存在的小根堆中
poll()：本质上就是 heapify 操作，首先弹出当前小根堆的根结点元素，并令剩余数字依旧保持小根堆结构。

但是其不能支持“修改堆中某个结构后以很轻的代价重新调整堆的结构”，只支持“弹出堆的根结点元素后重新调整堆的结构”，若想实现这些个性化的功能还需要自己定义堆结构。

其扩容机制是当 heapSize 快满时，将 heapSize * 2。这个操作的时间复杂度在每个元素平摊下来后其实很低

堆排序

堆排序的思想是：利用大根堆第一个元素最大的特性，令数组不断地组成大根堆，从而每次形成的大根堆里的第一个元素都是当前的最大值。

算法流程：

首先令当前数组的所有数字符合大根堆顺序（令一个数组变成大根堆的方式见后文，本质上就是不断做 heapInsert）
当前大根堆的根节点就是最大的元素，将其与数组的最后一个元素交换位置，此时即得到了整个数组最大的元素
接着将 heapSize–（因为已经有一个数字排好了序，heapSize 将减小），并对交换后的元素进行一次 heapify 操作：不断向下遍历子节点，直到与合适的位置数字进行交换。heapify 后，新的堆就又符合了大根堆结构
再取当前大根堆的根节点上的元素，它就是原数组第二大的数字，将其与大根堆结构中最后一个节点的元素进行交换。此时原数组中最后两个位置的元素就是最大和第二大的元素
再次 heapSize-- ，并对交换后的元素再进行一次 heapify 操作，新的大根堆的根结点的元素就是第三大的元素，将其与大根堆结构中最后一个节点的元素进行交换。
重复上述过程，直到大根堆的 heapSize == 0，此时即完成了排序

堆排序的复杂度：

时间复杂度是 O(N * logN)
额外空间复杂度 O(1)，只需要 swap 交换操作，不用开辟额外空间

代码：

public static void heapSort(int[] arr) {
  if (arr == null || arr.length < 2) {
    return;
  }

  // 1. 先将数组变为大根堆
  // 1.1 方式一: 依次将每个数字添加到堆结构中, 堆大小从0开始, 依次将新数字 heapInsert 进堆中
  // 编码思路是, 从前往后将每个节点进行 heapInsert
  // 其时间复杂度为 O(N*logN)
  for (int i = 0; i < arr.length; i++) {  // O(N)
    heapInsert(arr, i);                   // O(logN)
  }

  // 1.2 方式二: 从下向上, 先将每个子堆变为大根堆, 然后再将其父节点纳入再进行 heapify
  // 编码思路是, 从后往前将每个节点进行 heapify
  // 该方法速度更快, 其时间复杂度为 O(N)
  for (int i = arr.length - 1; i >= 0; i--) {
    heapify(arr, i, arr.length);
  }
  
  // 2. 每次将大根堆的根结点元素与最后一个元素交换
  int heapSize = arr.length;
  while (heapSize > 0) {                  // O(N)
    swap(arr, 0, heapSize-1);             // O(1)
    // 注意 heapSize 先减一再进入 heapify
    heapify(arr, 0, --heapSize);          // O(logN)
  }

  // 整体时间复杂度为 O(N*logN)
}

public static void heapInsert(int[] arr, int index) {
  // 向上遍历当前节点的父节点,直到满足条件: 父节点的值 > 当前节点的值
  while (arr[(index - 1) / 2] < arr[index]) {
    swap(arr, (index - 1) / 2, index);
    index = (index - 1) / 2; // index 记得变为父节点的值
  }
}

// heapSize 用于表示逻辑上的堆的大小, 其和数组的大小没关系
// 该方法的作用是, 在给定堆结构中, 当某个位置的元素被弹出,替换成了其他数字后
// 要保证新的数组仍然保持堆结构, 那么就需要从这个位置开始向下遍历
// 交换其子节点中最大的元素
public static void heapify(int[] arr, int index, int heapSize){
  if (heapSize > arr.length) {
    return;
  }

  while (2*index+1 < heapSize) {
    // 两个孩子中, 判断谁的值更大
    int largest = (2*index+2 < heapSize) && arr[2*index+1] < arr[2*index+2]
      ? 2*index+2 : 2*index+1;

    // 当前节点和子孩子中, 判断谁的值更大
    largest = arr[index] < arr[largest] ? largest : index;

    // 如果相等, 说明此时已经满足了大根堆的条件, 可以跳出循环
    if (largest == index) {
      break;
    }

    // 交换
    swap(arr, index, largest);
    index = largest;
  }
}

public static void swap(int[] arr, int a, int b) {
  if (a == b) {
    return;
  }

  arr[a] = arr[a] ^ arr[b];
  arr[b] = arr[a] ^ arr[b];
  arr[a] = arr[a] ^ arr[b];
}

补充：想让一组数字变成一个大根堆/小根堆结构，上文中的编码方式时间复杂度是 O(N * logN)。然后还有一种更快的方式令一个数组变为大根堆/小根堆结构，其时间复杂度为 O(N)

方式一：依次将每个数字添加到堆结构中，堆大小从0开始，依次将新数字 heapInsert 进堆中。当遍历完成后，即得到了大根堆，但这种方法的时间复杂度为 O(N * logN)
方式二：从下向上，先将每个子堆变为大根堆，然后再将其父节点纳入再进行 heapify。其时间复杂度为 O(N)（其时间复杂度的估计方法使用了错位相减法）

方式二就是一种逆向思维，反过来从后往前遍历数组，令其往后的子树符合大根堆，然后再向前遍历，不断扩大子树的大小，令新的子树也符合大根堆。这样的操作时间复杂度更低，因为整个树上一半的节点都是叶子节点，根本不需要做交换：

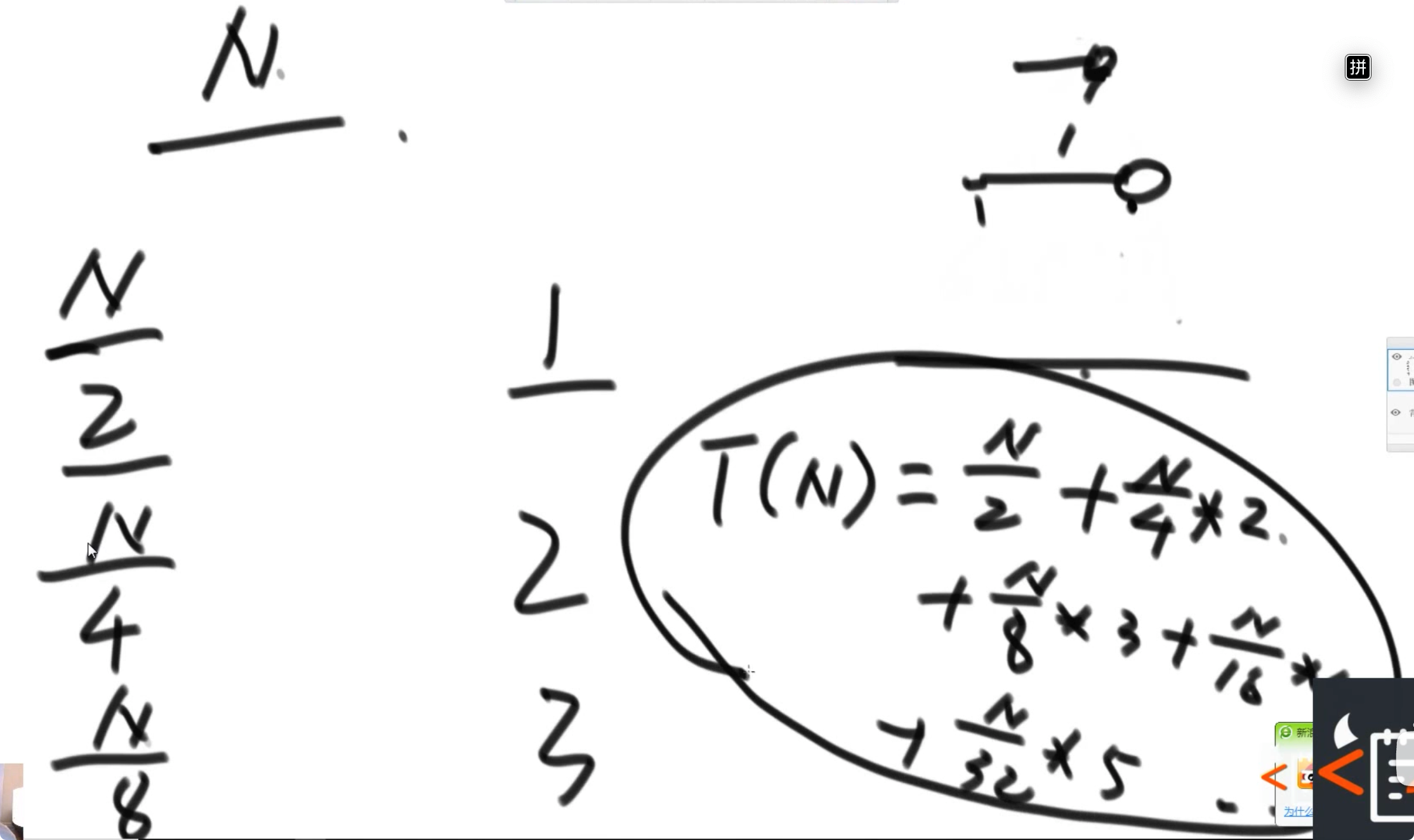
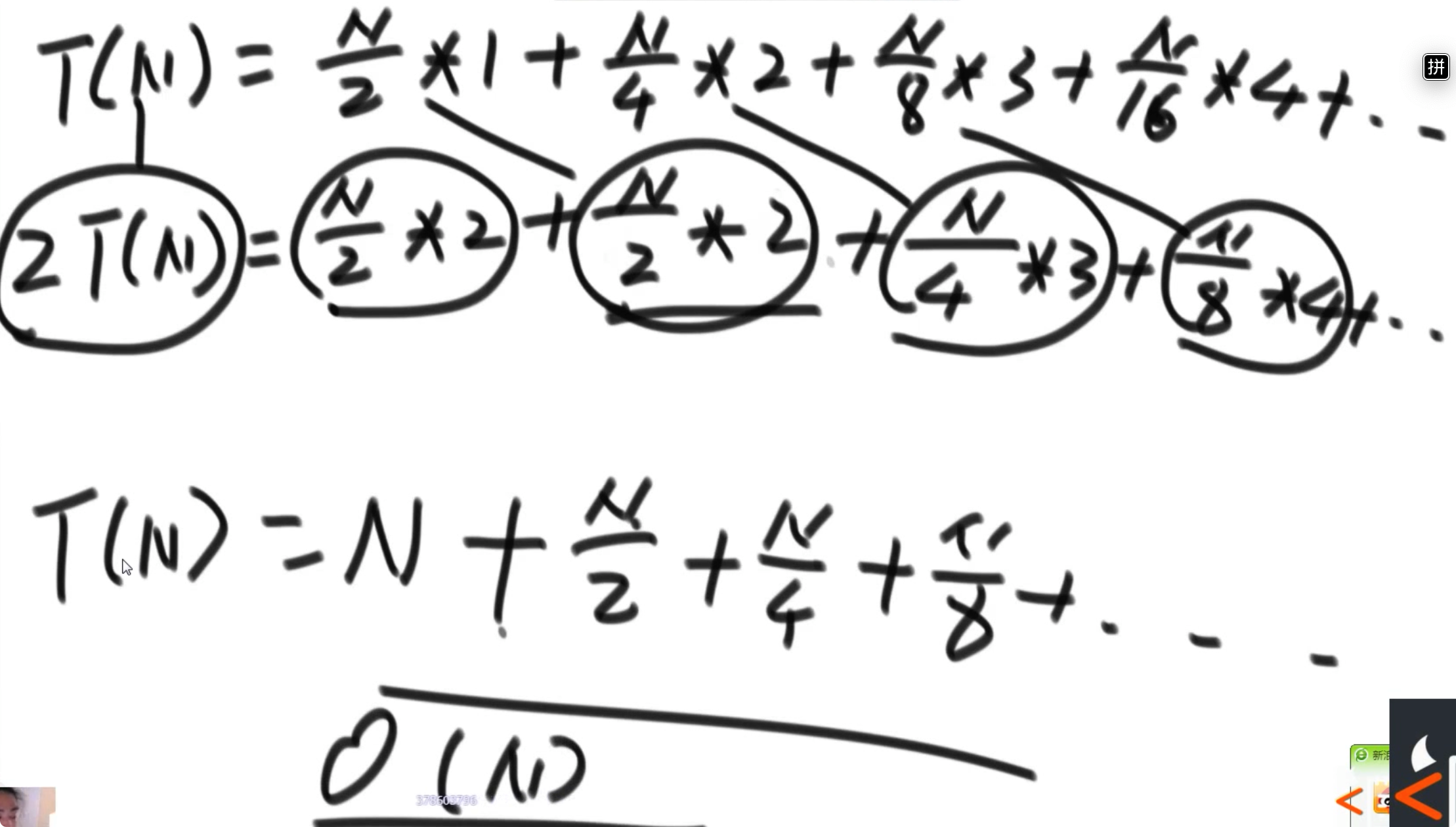
代码：

// 1. 先将数组变为大根堆
// 1.1 方式一: 依次将每个数字添加到堆结构中, 堆大小从0开始, 依次将新数字 heapInsert 进堆中
// 编码思路是, 从前往后将每个节点进行 heapInsert
// 其时间复杂度为 O(N*logN)
for (int i = 0; i < arr.length; i++) {  // O(N)
  heapInsert(arr, i);                   // O(logN)
}

// 1.2 方式二: 从下向上, 先将每个子堆变为大根堆, 然后再将其父节点纳入再进行 heapify
// 编码思路是, 从后往前将每个节点进行 heapify
// 该方法速度更快, 其时间复杂度为 O(N)
for (int i = arr.length - 1; i >= 0; i--) {
  heapify(arr, i, arr.length);
}

堆排序的扩展：几乎有序的数组

解题思路：这个移动距离不超过 k 非常重要，这意味着我们可以在 k 范围内组成一个小根堆，这个小根堆的第一个元素就是这个范围内的最小值，依次移动指针，将每个子 k 区域内的数组组成小根堆，即可不断得到当前范围内的最小值，从而完成排序。

具体流程：

首先取数组的前 k 个数字，组成小根堆（复杂度为 O(k * logk)，或用更快的方式可以达到 O(k)），然后将小根堆第一个位置的元素弹出，放到原数组的0位置，这个数就是整个数组的最小值（因为这道题限制了每个数字的移动距离不会超过 k）
接着向后移动1个位置，再取 k+1 位置上的数 arr[k+1] 与上一步剩下的 k-1 个元素一起再组成新的小根堆后，再取出最新小根堆里的第一个元素（此元素就是整个数组第二小的数）

重复上述过程，直到整个数组被遍历完，即可得到排序后的数组。此过程的时间复杂度为 O(N * logk)，如果这个k很小，那么这个算法的时间复杂度就比较接近 O(N)

具体实现既可以通过自己定义堆结构，又可以直接使用 Java 提供的优先级队列：PriorityQueue<Interger>，其底层就是一个小根堆结构。

小根堆在 Java 中就是优先级队列默认的实现方式： PriorityQueue<Interger>，其两个方法：

add() ：本质上就是 heapInsert 操作，将一个数字添加到已存在的小根堆中
poll()：本质上就是 heapify 操作，首先弹出当前小根堆的根结点元素，并令剩余数字依旧保持小根堆结构。

其扩容机制是当 heapSize 快满时，将 heapSize * 2。这个操作的时间复杂度在每个元素平摊下来后其实很低

若想实现大根堆，则只需要在创建优先级队列时传入自定义的比较器：

1 2	// 修改成大根堆 PriorityQueue<Integer> heap = new PriorityQueue<>((o1, o2) -> o2 - o1);

使用 PriorityQueue<Interger> 解该题：

package com.zhao;

import java.util.Arrays;
import java.util.PriorityQueue;

public class SortArrayDistanceLessK {
    public static void sortArrayDistanceLessK(int[] arr, int k) {
        if (arr == null || arr.length < 2) {
            return;
        }

        // 默认为小根堆
        PriorityQueue<Integer> heap = new PriorityQueue<>();

        // 0 ~ k-1 位置上的数组成小根堆(这里要取k和arr.length的最小值)
        for (int i = 0; i < Math.min(k, arr.length); i++) {
            heap.add(arr[i]);
        }

        int i = 0;
        for (; i < arr.length - k; i++) {
            arr[i] = heap.poll();
            // 注意索引值不是 i+k+1
            // 因为整个小根堆的heapSize==k, 所以 "当前根节点索引+k" 就是小根堆的下一个索引值
            heap.add(arr[i + k]);
        }

        // 上述遍历完毕后, 将大根堆里剩余的数挨个弹出放到数组的最后k个位置
        while (!heap.isEmpty()) {
            arr[i++] = heap.poll();
        }
    }

    public static void main(String[] args) {
        int[] arr = new int[]{2,3,1,5,4,6,8,7};

        SortArrayDistanceLessK.sortArrayDistanceLessK(arr, 3);
        System.out.println(Arrays.toString(arr));
    }
}

堆结构的常见问题

最小的 K 个数

https://leetcode-cn.com/problems/zui-xiao-de-kge-shu-lcof/solution/3chong-jie-fa-miao-sha-topkkuai-pai-dui-er-cha-sou/

剑指 Offer 40. 最小的k个数：输入整数数组 arr ，找出其中最小的 k 个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。

思路：我们用一个大根堆实时维护数组的前 k 小值。首先将前 k 个数插入大根堆中，随后从第 k+1 个数开始遍历，如果当前遍历到的数比大根堆的堆顶的数要小，就把堆顶的数弹出，再插入当前遍历到的数。最后将大根堆里的数存入数组返回即可。

代码：

// 1. 大根堆不断维护当前小的k个数字，当来新的数字，如果比堆顶大
//（比当前k个小数里的最大的小，说明这个最大的堆顶肯定不在答案里了），弹出堆顶
public int[] getLeastNumbers01(int[] arr, int k) {
    // 注意！！将系统默认的小根堆改成大根堆
    Queue<Integer> maxHeap = new PriorityQueue<>((o1, o2) -> o2 - o1);
    for (int i = 0; i < arr.length; i++) {
        if (i < k) {
            maxHeap.offer(arr[i]);
        } else {
            if (maxHeap.peek() > arr[i]) {
                maxHeap.poll();
                maxHeap.offer(arr[i]);
            } 
        }
    }

    int[] res = new int[k];
    int i = 0;
    // 弹出前k个元素
    while (!maxHeap.isEmpty()) {
        res[i++] = maxHeap.poll();
    }
    return res;
}

出现次数最多的前 K 个字符

给定一个字符串类型的数组，求其中出现次数最多的前 K 个。

思路：

先使用词频表统计每个字符出现的次数
创建一个小根堆，一直维护 K 个元素
遍历词频表的每一个位置：
- 如果当前小根堆堆顶元素小于当前值，则代表当前字符的词频更大，将堆顶元素弹出后，将当前位置放入堆中
- 如果当前小根堆堆顶元素大于当前值，则不放入
最后，依次弹出堆中的 K 个元素即可得到答案

代码：

public static class Node {
    public String str;
    public int times;

    public Node(String s, int t) {
        str = s;
        times = t;
    }
}

public static void printTopKAndRank(String[] arr, int topK) {
    if (arr == null || arr.length == 0 || topK < 1) {
        return;
    }
    HashMap<String, Integer> map = new HashMap<>();
    for (String str : arr) {
        if (!map.containsKey(str)) {
            map.put(str, 0);
        }
        map.put(str, map.get(str) + 1);
    }
    topK = Math.min(arr.length, topK);
    PriorityQueue<Node> heap = new PriorityQueue<>((o1, o2) -> o1.times - o2.times);
    for (Entry<String, Integer> entry : map.entrySet()) {
        Node cur = new Node(entry.getKey(), entry.getValue());
        if (heap.size() < topK) {
            heap.add(cur);
        } else {
            if (heap.peek().times < cur.times) {
                heap.poll();
                heap.add(cur);
            }
        }
    }
    while (!heap.isEmpty()) {
        System.out.println(heap.poll().str);
    }
}

数据流中的中位数

剑指 Offer 41. 数据流中的中位数：如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。

思路：建立一个 小根堆 A 和 大根堆 B ，各保存列表的一半元素，且规定：

A 保存较大的一半数字，长度为 N/2（N 为偶数时）或 (N + 1) / 2 （N 为奇数时）
A 保存较小的一半数字，长度为 N/2（N 为偶数时）或 (N - 1) / 2 （N 为奇数时）
每次添加一个新元素时，若需要加入到 A 中，则不能直接加入到 A，而是先加入到 B 中，令其重新调整后弹出 B 的堆顶后再加入到 A 中；加入到 B 同理

随后，中位数可仅根据 A, B 的堆顶元素计算得到。总结：A 中所有数字都比 B 中的大，并且当 N 为奇数时，A 中保存的数字个数比 B 多一个。

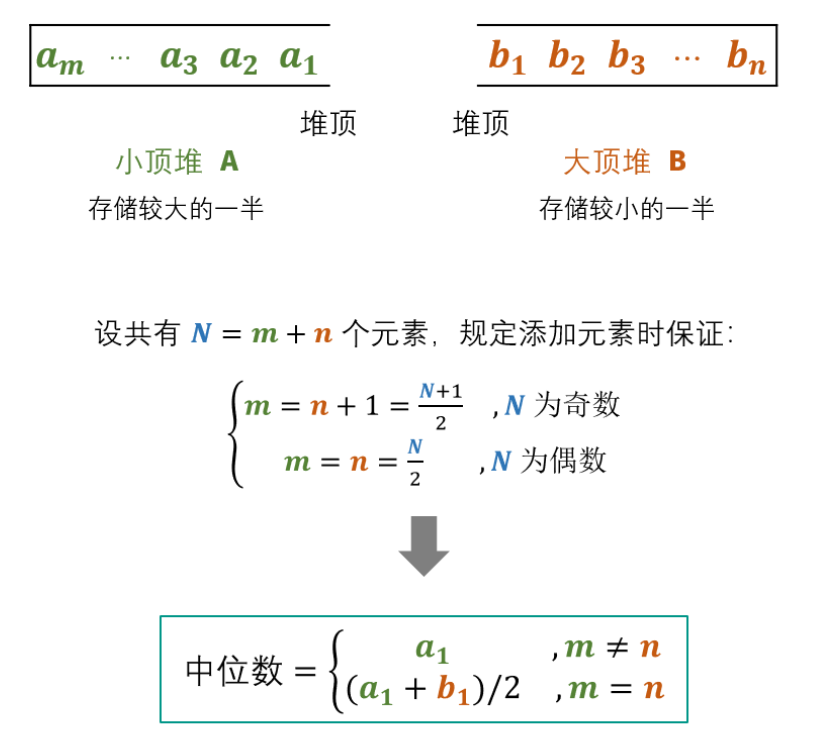
代码：

class MedianFinder {
    public PriorityQueue<Integer> A;
    public PriorityQueue<Integer> B = new PriorityQueue<>();

    public MedianFinder() {
        // A：保存较大的一半数，是一个小根堆
        A = new PriorityQueue<>();
        // B：保存较小的一半数，是一个大根堆
        B = new PriorityQueue<>((x, y) -> y - x);
    }

    public void addNum(int num) {
        // 如果 A 比 B 多，当前数字应该加入到 B 中
        if (A.size() > B.size()) {
            A.offer(num);
            B.offer(A.poll());
        } else {
            // 如果一样多，加到 A 中
            B.offer(num);
            A.offer(B.poll());
        }
    }

    public double findMedian() {
        return A.size() == B.size() ? 0.5 * (A.peek() + B.peek()) : A.peek();
    } 
}